在这篇文章中，我想谈谈颜色量化以及如何使用k-means聚类算法来执行它，以及优化其方法。 这里提供的代码是用python编写的，来自这个项目。
什么是颜色量化？
颜色量化是指一个减少在图像中的颜色数量的压缩过程。我们使用这种压缩过程的主要原因是在对仅支持有限数量颜色的设备（通常由于内存限制）中实现图像的渲染。
显然所有的压缩都会有（像素）损失。在这种情况下，生成的图像可能与原始图像的差异太大。因此，颜色量化的目标是获得与原始图像尽可能相似的压缩图像。实现这一点的关键因素是通过选择最能总结原始图像的颜色来选择调色（模）板。
最常见的技术将颜色量化的问题简化为点的聚类问题，其中每个点表示像素的颜色。它包括通过为每个集群选择所代表的点来创建调色板。之后，压缩简单地将所有颜色重新映射到它们的集群中。您可能猜到，所得到的调色板高度取决于所使用的颜色空间和距离度量。
在详细介绍调色板选择之前，先简单介绍颜色空间和色差。这个想法是要掌握一些概念，这些概念是必要的，用来了解接下来的内容，但并不会太详细，因为更详细的解释超出了本文的范围。如果你已经知道他们在说什么，请随意跳过这些部分。
颜色空间和色差
如先前预期的，颜色可以称为颜色空间的n维空间中的点。 最常见的是，空间是3维的，并且该空间中的坐标可以用于编码颜色。
存在用于不同目的和具有不同色域（颜色范围）的许多颜色空间，并且在它们的每一个中，可以定义量化色差的距离度量。 使用的最常见和最简单的距离度量是在RGB和Lab颜色空间中使用的欧几里得距离。
RGB颜色空间
RGB（红-绿-蓝的缩写）颜色空间是迄今为止最常见和广泛使用的颜色空间。 想法是，通过结合红色，绿色和蓝色来创建颜色。 RGB中的颜色通常被编码为每个8位的3元组，因此每个维度采用在范围[0，255]内的值，其中0表示没有颜色，255表示全部的颜色。
如前所述，在RGB中，我们可以使用欧几里得距离来计算两种颜色之间的差异：
在RGB颜色空间中使用欧几里得距离的一个不足的是，它与眼睛感知的差异不一致。换句话说，即使两对颜色具有相同的欧几里得距离，也可能感觉上色差不一样大。如果我们用d′感知的差异，我们计算颜色对之间的差异(R1,G1,B1),(R2,G2,B2)和(R1,G1,B1),(R2,G2,B2)我们可以得到:
这是因为人眼对某些颜色比其他颜色更敏感。
Lab颜色空间
Lab颜色空间，更正式的说法:L∗a∗b∗，其包括了所有可感知的颜色，这意味着其色域是RGB颜色空间色域的超集，并且感知均匀。因此解决使用欧几里得距离时RGB颜色空间带来的与感知不一致的问题。 在Lab的情况下，这个距离被称为CIE76，并且用ΔE∗76（CIE代表国际照明委员会）表示它:
L*维表示颜色的亮度，并且其值在[0,100]中，其中越亮者越高。 a*和b*是色对立维度，其中a*表示负值的绿色和正值的红色，而b*表示负值的蓝色和正值的黄色。 对于a*和b*，0的值表示中性灰色，它们的范围取决于Lab的实现，但通常是[-100,100]或[-128,127]。
其他颜色空间
仍然有许多其他颜色空间，即使它们不会在下一节被用于执行颜色量化。不过，值得一提的是L*C*h*颜色空间，为了解决在使用ΔE∗76中的问题，CIE定义了在L*C*h*色彩空间中的ΔE∗94和ΔE∗00。 不过无论如何，这两个距离都不是基于简单的欧几里得距离。
调色板选择
我们现在可以开始执行颜色量化，看看输出如何根据使用的颜色空间，创建调色板的方法以及我们想要构建的调色板的大小变化而改变的。
为了方便比较，我们将使用Lenna的图像：
随机选择
最简单的选择调色板的方法是随机选择。在构建调色板之后，每种颜色被重新映射到作为该选择部分的最近的颜色。你可能可以猜到，使用RGB或Lab空间没有什么区别，影响最终输出的唯一的事情是使用的颜色数量。如果使用这种选择策略，似乎一个颜色空间看起来比另一个颜色空间表现更好。记住，在给定随机选择的情况下，这只是一种特例。
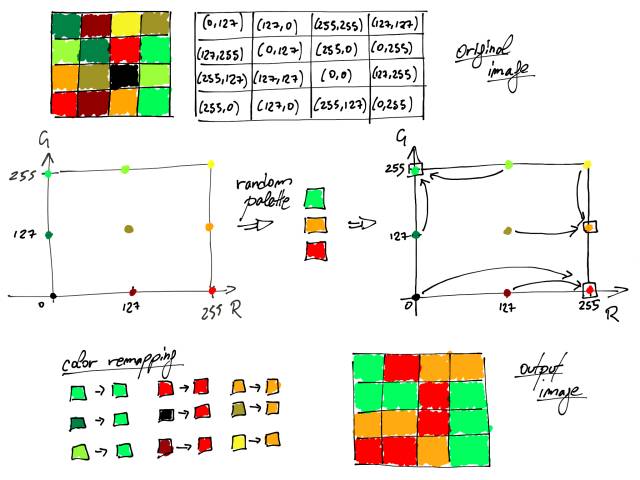
在下图中，它在视觉上解释了在RGB空间的情况下的整个过程，其中最终的调色板由三种颜色组成（对于Lab空间是完全类似的）。为了简单起见，在该示例中，蓝色通道被固定为值0，因此我们可以仅考虑R和G维度。图像的所有像素都用RGB编码表示，然后映射到RGB空间。然后选择3个随机颜色作为调色板的一部分。最后，根据欧几里德距离将所有颜色重新映射到最接近的所选颜色。
在RGB空间中使用随机选择
这里通过随机选择RGB颜色空间中的颜色产生的输出图像。 它们的调色板分别由8,16,32和64种颜色组成。
在Lab空间中使用随机选择
这里通过随机选择Lab颜色空间中的颜色而产生的输出图像。 在这种情况下，它们的调色板分别由8,16,32和64种颜色组成
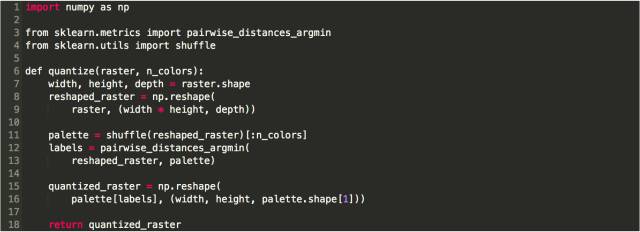
通过随机选择的调色板来实现颜色量化是非常容易的。 在以下代码中，输入变量raster 和输出变量quantized_raster都是 numpy.ndarray，它们分别对应于原始图像的光栅和量化图像的光栅。 它们都可以用RGB或Lab编码（输出栅格具有与输入相同的编码），并具有(width, height, 3)的形式。
可以通过将文件的路径传递到scipy来检索图像的栅格
scipy.misc.imread的输出是一个numpy.ndarray，其形式为(width,height,3)，其值为RGB编码。 因此，为了在Lab空间中执行量化，我们首先需要将RGB转换为Lab。 借助skimage，我们可以将RGB转换为Lab，反之亦然：
最后，为了可视化颜色量化的结果，我们可以使用matplotlib来绘制:
请注意，imshow函数仅适用于在[0,1]间隔中规范化的RGB值，这就是为什么我们需要除以255.
用k-means选择
如在开始时所预期的，执行颜色量化的一种常见方法是使用聚类算法。在这种情况下，我们将使用k-means的最小化集群内的质心和其他点之间的距离之和，来进行量化。假设k-means聚类算法使用的距离是欧几里得距离，则它是适用于与RGB和Lab空间两者的颜色量化的自然拟合。为了这篇文章的目的，我先假设你知道k-means如何工作。
该过程包括应用具有多个质心的k-means算法，所述的质心（数量）指我们想要调色板被组成的颜色的数量。然后我们使用得到的质心作为调色板的一部分的颜色。之后，如在随机选择中那样，将每种颜色重新映射到调色板中的那些中最接近的一个。在给定k-means的性质下，最近的颜色将准确地对应于其一部分聚类的质心所代表的颜色。
重要的是，具有相同颜色的图像中的n个像素在颜色空间中包括n个重叠点，而不在单个点中。实际上在随机选择的情况下它没有差别，但是当应用k-means算法时它有很多差别。
请记住，Lab空间中的欧氏距离是均匀的，差异是由人眼感知的。因此，通过这种选择，我们可以期望使用Lab空间应该具有比RGB更好的视觉效果。
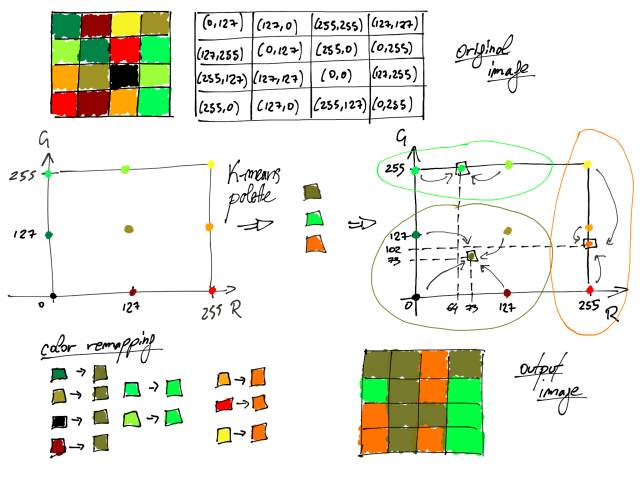
类似于下面的其他图，它在视觉上解释了RGB空间情况下的整个过程，但使用的是k-means算法。 即使在本示例中，最终调色板也是由三种颜色组成，为了简单起见，蓝色通道固定为值0。图像的所有像素用RGB编码表示，然后如在随机选择的情况下映射到RGB空间中。 然后应用K-means算法，并且聚类的质心被选择为调色板的一部分。 最后，如在随机调色板选择中，根据欧几里得距离将所有颜色重新映射到最接近的所选颜色。
在RGB空间中使用k-means
这里由使用k-means在RGB颜色空间中生成的输出图像。 它们的调色板分别由8,16,32和64种颜色组成。
在Lab空间中使用k-means
在Lab颜色空间中用k-means生成的输出图像。 在这种情况下，它们的调色板分别由8,16,32和64种颜色组成。
代码
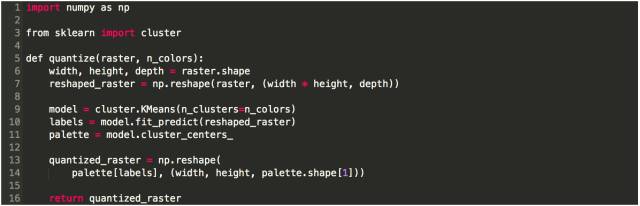
这里是使用k-means算法来执行颜色量化的代码。以下函数具有与用随机选择的函数相同的功能，并且已经讨论过的关于光栅加载，颜色空间转换和结果可视化的内容仍然适用。
结论
我们可以看出，使用k-means好于使用简单随机选择。事实上，使用64种颜色的随机选择获得的图像与使用具有32种颜色的k-means获得的图像非常相似。使用k-means的缺点是，显然它明显更慢，特别是如果训练时用原始图像，那么所有像素都要执行一遍的。不过这可以通过仅使用像素的随机样本来降低。
另一方面，乍一看，在RGB空间中的k-means和在LAB空间中的k-means的结果是相似的。不过，通过仔细观察每一对图像，在某些情况下，特别是在处理某些细节时，我们可以说，一个比另一个更好。但一般对于特定图像来说，当使用RGB时，脸部看起来更清晰，也更明确，并且尤其对前两张图像。然而，使用LAB空间似乎对镜子和帽子的反射处理的更好，它还还原了原始图像的亮度。总的来说，我不会说：“当使用k-means时某一个颜色空间比另外一个更好，至少对于这张图片不会。”