1 前言
聚类常用于数据探索或挖掘前期,在没有做先验经验的背景下做的探索性分析,也适用于样本量较大情况下的数据预处理等方面工作。例如针对企业整体用户特征,在未得到相关知识或经验之前先根据数据本身特点进行用户分群,然后再针对不同群体做进一步分析;例如将连续数据做离散化,便于做后续分类分析应用。
KMeans是聚类方法中非常常用的方法,并且在正确确定K的情况下,KMeans对类别的划分跟分类算法的差异性非常小,这也意味着KMeans是一个准确率非常接近实际分类的算法。本文将讨论如下基于自动化的方法确立K值。
本案例是《Python数据分析与数据化运营》中“7.11案例-基于自动K值的KMeans广告效果聚类分析”的一部分,其ad_performance.txt和源代码chapter7_code2.py位于“附件-chapter7”中,该附件可以在可从http://www.dataivy.cn/book/python_book.zip或https://pan.baidu.com/s/1kUUBWNX下载。
2 实现思路
K值的确定一直是KMeans算法的关键,而由于KMeans是一个非监督式学习,因此没有所谓的“最佳”K值。但是,从数据本身的特征来讲,最佳K值对应的类别下应该是类内距离最小化并且类间距离最大化。有多个指标可以用来评估这种特征,比如平均轮廓系数、类内距离/类间距离等都可以做此类评估。基于这种思路,我们可以通过枚举法计每个K下的平均轮廓系数值,然后选出平均轮廓系数最大下的K值。
3 核心过程
假设我们已经拥有一份预处理过的数据集,其中的异常值、缺失值、数据标准化等前期工作都已经完成。下面是完成自动K值确定的核心流程:
score_list = list() # 用来存储每个K下模型的平局轮廓系数
silhouette_int = -1 # 初始化的平均轮廓系数阀值
for n_clusters in range(2, 10): # 遍历从2到10几个有限组
model_kmeans =KMeans(n_clusters=n_clusters, random_state=0) # 建立聚类模型对象
cluster_labels_tmp =model_kmeans.fit_predict(X) # 训练聚类模型
silhouette_tmp =metrics.silhouette_score(X, cluster_labels_tmp) # 得到每个K下的平均轮廓系数
if silhouette_tmp >silhouette_int: # 如果平均轮廓系数更高
best_k =n_clusters # 将最好的K存储下来
silhouette_int =silhouette_tmp # 将最好的平均轮廓得分存储下来
best_kmeans =model_kmeans # 将最好的模型存储下来
cluster_labels_k =cluster_labels_tmp # 将最好的聚类标签存储下来
score_list.append([n_clusters, silhouette_tmp]) # 将每次K及其得分追加到列表
print ('{:*^60}'.format('K value and silhouette summary:'))
print (np.array(score_list)) # 打印输出所有K下的详细得分
print ('Best K is:{0} with average silhouette of{1}'.format(best_k, silhouette_int.round(4)))该步骤的主要实现过程如下:
定义初始变量score_list和silhouette_int。score_list用来存储每个K下模型的平局轮廓系数,方便在最终打印输出详细计算结果;silhouette_int的初始值设置为-1,每个K下计算得到的平均轮廓系数如果比该值大,则将其值赋值给silhouette_int。
提示:对于平均轮廓系数而言,其值域分布式[-1,1]。因此silhouette_int的初始值可以设置为-1或比-1更小的值。
使用for循环遍历每个K值,这里的K的范围确定为从2-10.一般而言,用于聚类分析的K值的确定不会太大。如果值太大,那么聚类效果可能不明显,因为大量信息的都会被分散到各个小类之中,会导致数据的碎片化。
通过KMeans(n_clusters=n_clusters, random_state=0)建立KMeans模型对象model_kmeans,设置聚类数为循环中得到的K值,设置固定的初始状态。
对model_kmeans使用fit_predict得到其训练集的聚类标签。该步骤其实无需通过predict获得标签,可以先使用fit方法对模型做训练,然后使用模型对象model_kmeans的label_属性获得其训练集的标签分类。
使用metrics.silhouette_score方法对数据集做平均轮廓系数得分检验,将其得分赋值给silhouette_tmp,输入参数有两个:
- X:为原始输入的数组或矩阵
- cluster_labels:训练集对应的聚类标签
接下来做判断,如果计算后的得分大于初始化变量的得分,那么:
- 将最佳K值存储下来,便于后续输出展示
- 将最好的平均轮廓得分存储下来,便于跟其他后续得分做比较以及输出展示
- 将最好的模型存储下来,这样省去了后续再做最优模型下fit(训练)的工作
- 将最好的聚类标签存储下来,这样方便下面将原始训练集与最终标签合并
每次循环结束后,将当次循环的K值以及对应的评论轮廓得分使用append方法追加到列表。
最后打印输出每个K值下详细信息以及最后K值和最优评论轮廓得分,返回数据如下:
**************K value and silhouette summary:*************** [[ 2. 0.46692821] [ 3. 0.54904646] [ 4. 0.56968547] [ 5. 0.48186604] [ 6. 0.45477667] [ 7. 0.48204261] [ 8. 0.50447223] [ 9. 0.52697493]] Best K is:4 with average silhouette of 0.5697
上述结果显示了不同K下的平均轮廓得分。就经验看,如果平均轮廓得分值小于0,意味着聚类效果不佳;如果值大约0且小于0.5,那么说明聚类效果一般;如果值大于0.5,则说明聚类效果比较好。本案例在K=4时,得分为0.5697,说明效果较好。
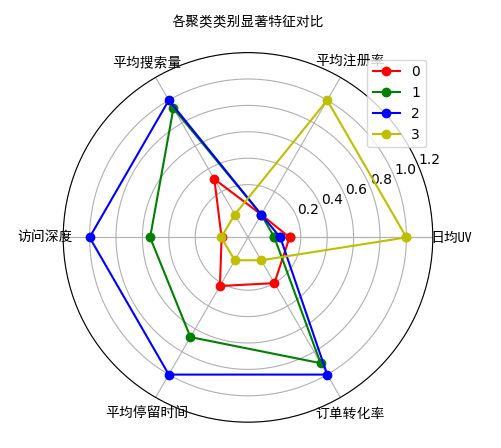
对于上述得到的结果,将最优K值下得到的KMeans模型的结果,可以通过各类别的类内、外数据的对比以及配合雷达图或极坐标图做分析解释。
各聚类类别显著特征对比
4 引申思考
注意,即使在数据上聚类特征最明显,也并不意味着聚类结果就是有效的,因为这里的聚类结果用来分析使用,不同类别间需要具有明显的差异性特征并且类别间的样本量需要大体分布均衡。而确定最佳K值时却没有考虑到这些“业务性”因素。
案例中通过平均轮廓系数的方法得到的最佳K值不一定在业务上具有明显的解读和应用价值。如果最佳K值的解读无效怎么办?有两种思路:
- 扩大K值范围,例如将K的范围调整为[2,12],然后再次运算看更大范围内得到的K值是否更加有效并且能符合业务解读和应用需求。
- 得到平均轮廓系数“次要好”(而不是最好)的K值,再对其结果做分析。
对于不同类别的典型特征的对比,除了使用雷达图直观的显示外,还可以使用多个柱形图的形式,将每个类别对应特征的值做柱形图统计,这样也是一个非常直观的对比方法。具体参考下图: