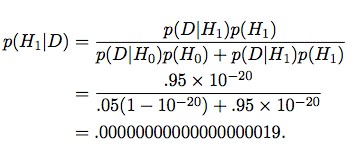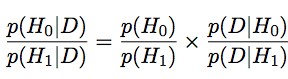最近看到一篇很有意思的博文,关于统计学在心理学中应用引发的讨论。想到平时我们生物信息学分析数据的时候,往往很多结论和推断都是基于统计学意义上进行的,看到这篇博文觉得挺有意思,与生物信息人同飨。下面是博文原文:
今天后知后觉地读到一年前在心理学界掀起一片哗然的文章:
作者康奈尔大学心理学教授 Bem 在文中声称普通人有预知未来的能力。具体可参阅科学松鼠会当时的报道。文章用9个实验证明,发生在未来的事情会对被试者之前的判断产生影响,且其中8个实验都具有统计显著性。
那么这样的统计显著性是怎么算出来的呢?
Wagenmakers等人 back to back 发表于同一期杂志的评论文章指出了上述文章的3大谬误:
1. 混淆了确认性研究和探索性研究
确认性研究就是,在进行实验之前已经有明确的假说。比如假说是,发生在未来的单词背诵练习会提高之前的自由回忆的准确率。然后收集实验数据,进行单次统计检验。
探索性研究就是,没有明确的假说,进行各种能想到的实验,从中找出有统计显著性的结果。这会导致多重比较 (Multiple comparisons) 的问题。比如检验一种新药是否对疾病症状有所改善,如果检验许多种症状,则很有可能其中某种症状表现出显著改善。借用维基百科 Multiple comparisons 文中的例子,如果扔一枚硬币10次其中9次以上都出现正面,那我们会怀疑这个硬币有偏倚,因为如果这个硬币没偏倚,10次出现9次以上正面的概率是 (10 + 1) × (1/2)10= 0.0107,确实不太可能。那么假设我们抛100枚不同的硬币,都没有偏倚,但是其中1个或以上硬币出现9次以上的概率是 1 - (1 − 0.0107)100 ≈ 0.66,就是说,我们很有可能得出结论说其中某一枚硬币有偏倚,虽然指定的硬币A有偏倚的概率仍然是 0.0107。
Bem 的研究中,多次使用多重比较,但是没有对单次检验的显著性水平进行修正,因此高估了显著性。
2. 条件概率倒置谬误(Fallacy of the transposed conditional)
统计检验得出的 p-value,并没有告诉我们我们想要的答案。我们想知道的是:“给定这些数据,H0 为真的概率 p(H0|D)。但实际上 p-value 表示的是,给定 H0 为真,出现这些数据的概率 p(D|H0)。正如 Jacob Cohen 在1994年指出的,这二者是不同的。
对 p-value的错误解读也许是这么来的:
如果 H0 正确,出现这些数据不太可能。
这些数据出现了。
所以, H0 不太可能是正确的。
乍一看来,上面的论述和逻辑学里面的否定后件(modus tollens)差不多:
火星人不是五毛党。
这个人是五毛党。
所以,他不是火星人。
上述推论没任何问题。但是当第一句话换成概率而不是绝对确定时:
一个中国人不太可能是五毛党。(五毛党占人口比例应该不高,但愿小于5%)
这个人是五毛党。
所以,他不太可能是中国人。(什么?外国人那是5美分党好不好)
那些错误理解 p-value 的人,应该蹲在墙角哭去了。
在 Bem 的文章里,他有意或无意滴错误解读了 p-value。文中,H0 是人不能预知未来,H1 是人可以预知未来。但由于H1 为真的先验概率无比的低,首先没有任何物理学和生物学的证据,其次如果H1 为真,人就可以靠预知未来在赌场发大财了(详见Wagenmakers等的估算)。因此假定 p(H1) = 10-20。那么 p(H0) = 1 – 10-20。假设一个设计正确的实验得到的数据更可能在 H1 为真时出现,比如说是 H0 为真时的19倍。那么我们真正想知道的 p(H1|D) 可以如下计算
虽然这个后验概率比先验概率 p(H1) = 10-20 高了不少,但仍然不足以证明人可以预知未来。
3. p-value 高估了证伪 H0 的证据
举个例子,比如说你中了彩票,别人说你作弊,因为中彩票是小概率事件。但是与中彩票相比,通过不法手段不正当关系提前得知中奖号码的概率更小(在大多数国家)。
因此,如果想用数据证伪 H0 ,需要和 H1 相比较。虽然在 H0 为真时得到这些数据的概率很小,也许在 H1 为真时概率同样很小。
我们需要比较的是,
用文字表述就是,
后验模型可能性 = 先验模型可能性 x 贝叶斯因子
(Posterior model odds = prior model odds x Bayes factor)
贝叶斯因子可以解释为数据带来的权重变化。
简单的说,如果 Bem 要证明预知未来的假说为真,贝叶斯因子需要在10-24 数量级,而他的实验中,基本都在1上下,最小不过0.17。因此完全不能证伪 H0 或证实 H1。
最后的话
其实我想说的是,如果想发文章,只要很好的发扬上述3个谬误就可以啦。事实上目前心理学、医学界一些文章都是这样做的,包括生物学文章里的统计部分(还好生物还有很多细胞果蝇线虫老鼠跑胶测序染色切片等等统计不可替代的部分)。
当然,如果明知故犯也不太好,但是如果真的做到设计实验统计都完美无缺,那基本是很难有显著性结果了。有个流行词叫 发表偏倚 (Publication bias),就是说发表的结果大多是有统计显著性的,而其实也许每一个发表的显著性研究背后,都有99个被扔到废纸篓里的统计不显著研究(还记得多重比较么)。这就是为啥一些声称有效的疗法、声称显著的实验,却不能被重复的原因。
相关文献:
Bem, D. J. (2011). Feeling the future: Experimental evidence for anomalous retroactive influences on cognition and affect. Journal of Personality and Social Psychology, 100, 407-425.
Wagenmakers, E.-J., Wetzels, R., Borsboom, D., van der Maas, H. L. J. (2011). Why psychologists must change the way they analyze their data: The case of psi: Comment on Bem. Journal of Personality and Social Psychology, 100, 426-432.
Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49, 997-1003.
本文来自:http://azaleasays.com/2012/07/05/statistics-guarantees-publications/