N50 statistic is widely used by bioinformaticians to judge the quality of their assemblies, but it is a faulty measure. Possibly in recognition of that fact, one of the stated goals of Assemblathon is to “produce newer metrics for assessing the quality of a genome assembly that will complement existing statistics such as N50 contig size”. What is wrong with N50 and how can it be improved?
Let us first explain, how N50 came to be accepted as a good measure for comparing assembly qualities. N50 measures the ‘average’ sizes of long scaffolds in an assembly by taking into fact that a genome assembly has few very long scaffolds and many tiny scaffolds. It works well provided the genome assembly is mostly error-free.
Overlap-layout-consensus assembly programs developed for Sanger sequences filtered out the repetitive regions, assembled the remaining reads based on their mutual overlaps, and then linked together the contigs into longer scaffolds using mate pairs. Although misassemblies were always present to some extent, having large number of incorrect junctions was less likely in such a pipeline provided the repetitive regions were filtered properly.
The de Bruijn graph-based assemblers used for NGS libraries are different, because the graphs do not exclude k-mers from repetitive regions. In a broad sense, a de Bruijn graph of a genome has three types of k-mers -
(i) those from the unique regions of the genome and having unique neighbors in the graph,
(iii) those from non-unique or repetitive regions of the genome.
Assembling the first group is easy. The second group was discussed in this commentary, and they can be resolved by additional assembly step such as varying k-mer size or going through the reads, as Chrysalis step in Trinity does. Resolving the third group is not easy, and may sometimes be mathematically impossible based on given data.
The problem with the third group is not that they provide no path of traversal through the graph, but that they provide too many paths. An aggressive assembly technique may try to resolve the third group by picking one path out of many, and thus may get higher N50. However, that N50 is a product of introducing many incorrect junctions. There is no limit to how many incorrect junctions can be present in an assembly produced from de Bruijn graph, because all k-mers from repetitive regions are present in the graph.
What could be a good measure along with N50 to judge the quality of an assembly? Ideally, it should be the number of erroneous junctions made in the assembly, but that is impossible to do without knowing what the correct sequence is, whereas knowledge of the correct sequence is not possible a priori in an assembly problem.
Here is our proposed solution for a good metric.
Count the k-mer distribution of the assembly and compare it with the k-mer distribution expected from the reads. Some preliminary thoughts on how it would work was presented in this commentary, but let us elaborate further.
Let us say a k-mer ‘ATGGGGGGTTAT’ appears 20 times in an assembled genome, whereas it is expected to be an unique k-mer based on k-mer count from the reads. We can say for sure that the k-mer is wrongly assembled. The same calculation can be repeated for all k-mers in the assembly, and an aggregate measure would express how incorrect the placement of various k-mers is.
The above k-mer correctness metric along with N50 can tell us to some extent whether the high N50 is achieved with mostly correct junctions, or with many incorrect junctions. We will elaborate on it further in a later commentary.
In the above, we discussed why N50 is a faulty measure of assembly quality. It can reward an aggressive assembler (or assembly strategy) that chooses one of many paths suggested by k-mers from repetitive regions to get high N50, but also higher number of incorrect junctions. The proposed solution was to augment N50 with another measure that compares expected k-mer distribution with observed k-mer distribution.
How does the measure work? In the Figure 1 below （ From“Maximizing Utility of Available RAMs in K-mer World”）, we presented the k-mer (k=21) distribution of a genome and showed that most 21-mers are present only once in the genome, a small number of 21-mers are present twice, and so on.
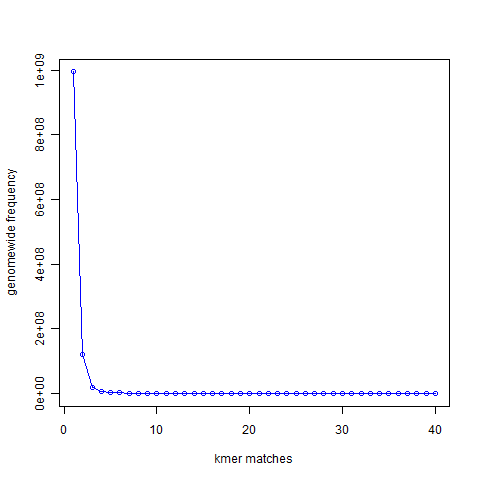
Figure 1
The Figure 2 presented 21-mer distribution of simulated reads chosen from the same genome with the genome being sampled roughly 50 times. The peak representing unique 21-mers in the first figure moved to 40 in the second figure. The peak representing 21-mers present twice in the first figure moved to 80 and so on, because the reads were sampling the genome many times.
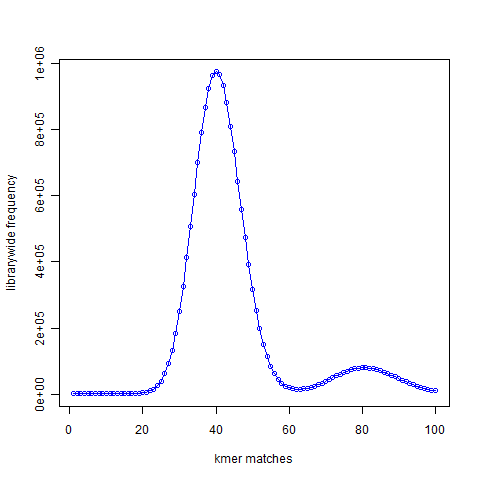Figure 2
Given a set of NGS reads, the second figure is easy to construct. From the position of the peak at 40 (or at other region), it is possible to rank each k-mers as ‘unique’, ‘present twice’, ‘present thrice’, etc. That will represent the expected distribution of the k-mers.
Similarly, a version of the first figure is possible to construct from the de Bruijn graph-based assembly of the NGS library. From the assembly, it is possible to compute observed k-mer distribution of the corresponding k-mers.
If an assembly is correct, those two k-mer distributions should match as closely as possible. Therefore, any discrepancy reflects errors in the assembly. I can think of some exceptions in case of SNPs or haplotype differences, but for most genomes those factors come as as second order differences.
The readers may object that the above method does not directly address the question of incorrect junctions. That criticism is indeed true. However, if an assembler incorrectly connects contig A with B and C with D, whereas A should be connected to C and B with D, the assembler does not get high N50. It is possible to high N50 by an aggressive assembler, only if it traverses through the same repetitive region more often than reality and interconnects more contigs than reality.
From:
http://www.homolog.us/blogs/2012/06/26/what-is-wrong-with-n50-how-can-we-make-it-better/
http://www.homolog.us/blogs/2012/06/26/what-is-wrong-with-n50-how-can-we-make-it-better-part-ii/