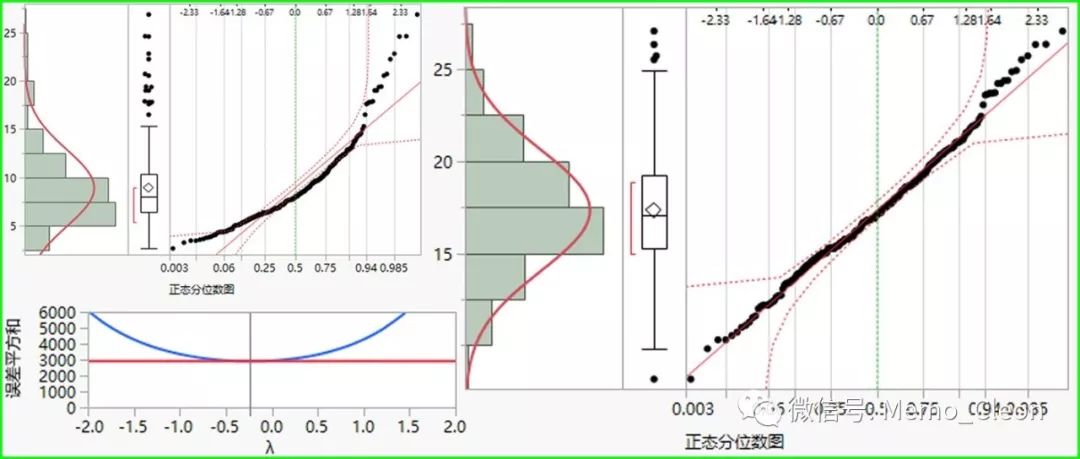
当资料不满足正态分布时,教科书里常常说可以通过变量变换将原始数据做某种函数的转换,常用的变量变换有对数变换、平方根变换、平方根反正弦变换、倒数变换等,这些变换有各自适用的数据,需要多次尝试来寻找合适的变换。适当的变换可同时满足正态化和方差齐性的要求。但对像我这种数学不好的人,选择用哪种变换的确是一件挺难的事。
实际中常用Box-Cox变换,Box-Cox变换是多种变换的统称,表达式为:
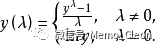
通过Box-Cox变换后可寻找到最佳的λ值,再根据λ值对因变量进行变换。
但经过数据变换后,在结果的解释上不如原始数据方便。
示例:272立儿童年龄与白细胞值得关系。
SPSS过程可参见正态分布与方差齐性的检验方法与SPSS操作,结果显示数据不呈正态分布。

【1】JMP检验正态分布步骤及结果解读
分析>>分布:将“白细胞”选入Y列,确定;
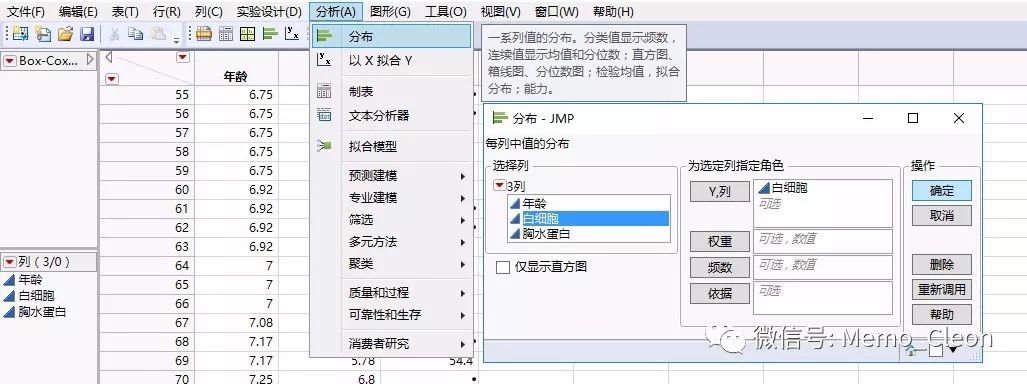
“白细胞”旁红三角菜单>>正态分位图;
“白细胞”旁红三角菜单>>连续拟合>>正态;
在结果正态拟合部分,点击“正态拟合”旁红三角菜单>>拟合优度。
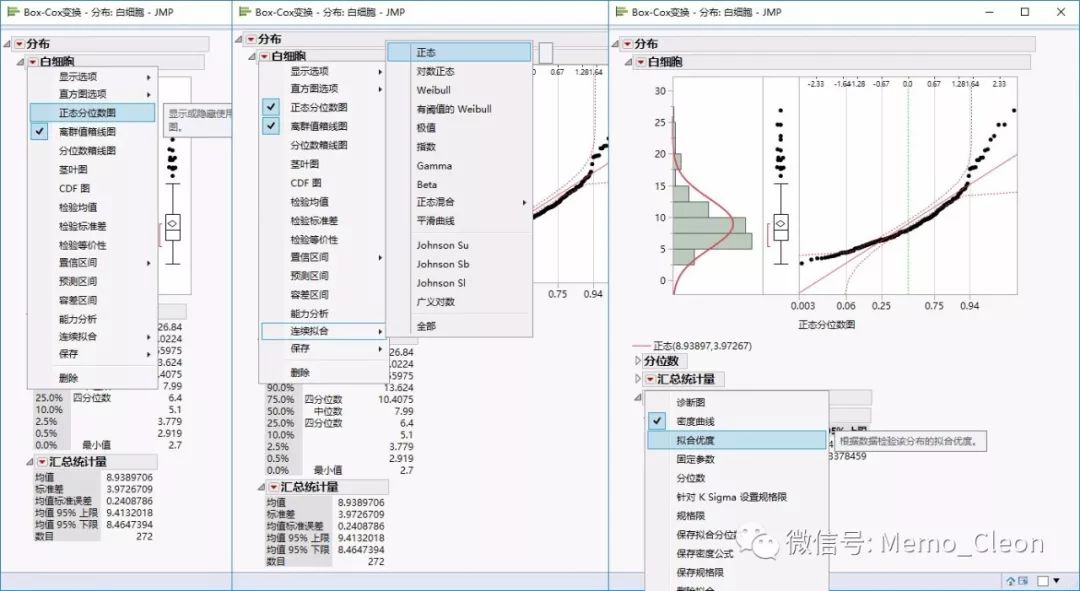
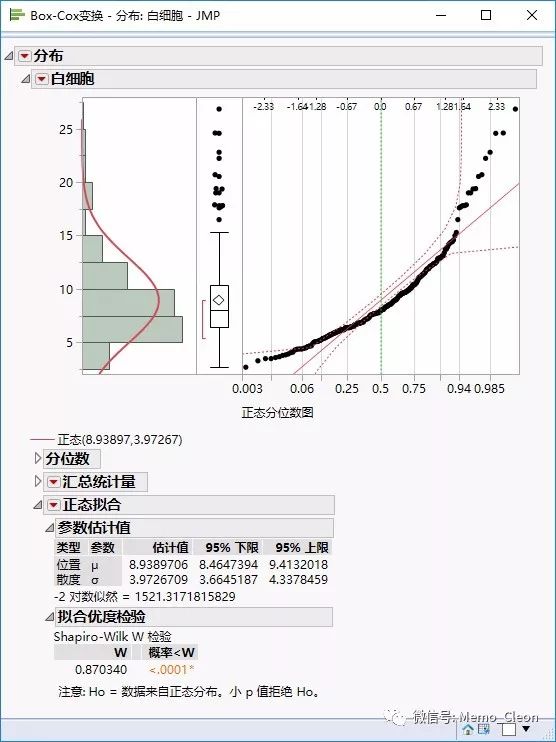
结果如下:
正态分位图部分:数据点并没有全部收敛在95%置信限内说明,说明数据不服从正态分布。拟合优度检验:Shapiro-Wilk W检验,W=0.870,P<0.001,数据不服从正态分布,同SPSS结果完全一致。
【2】Box-Cox变换,首先寻找最佳λ值
分析>>拟合模型:将“白细胞”选入Y列,确定;
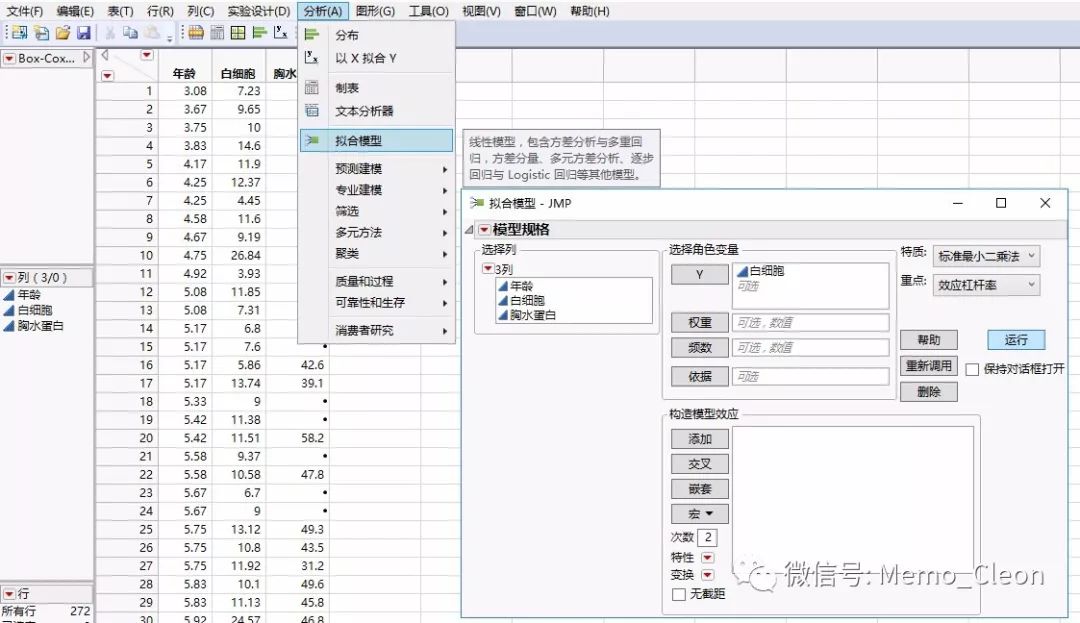
“响应‘白细胞’”旁红三角菜单>>因子刻画>>Box-Cox Y变换。结果显示当λ=-0.233时,变换后的数据更接近正态分布。
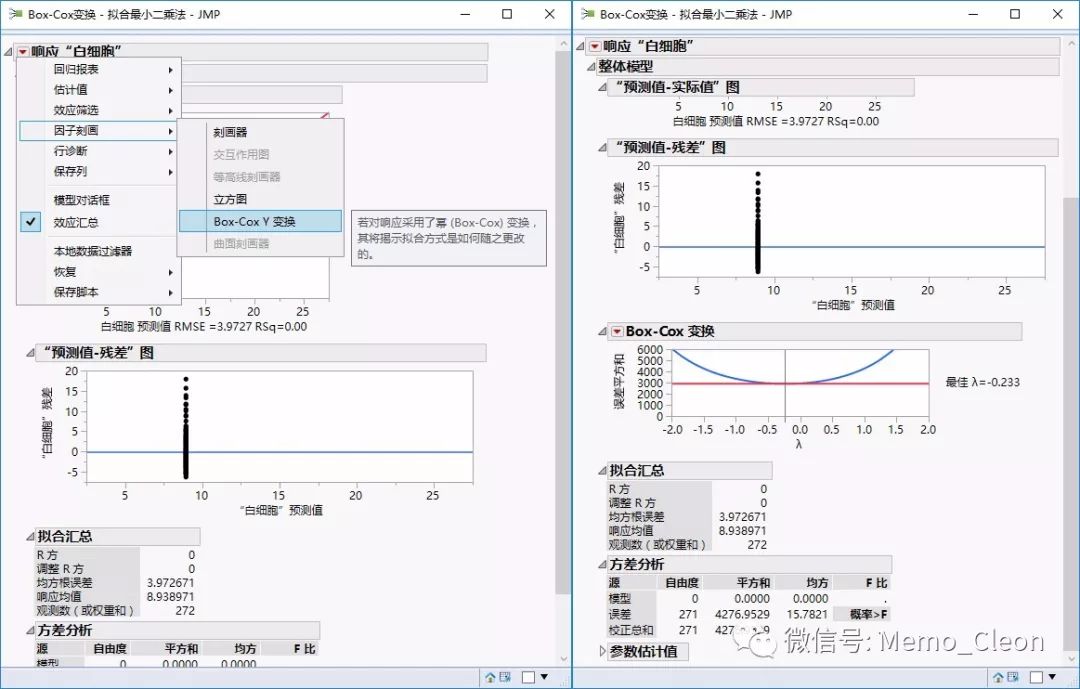
【3】考察变换后数据的正态性
“Box-Cox变换”>>保存最佳变换;
“Box-Cox变换”>>保存特定变换。在弹出的“请输入数值”对话框中,为Box-Cox公式输入λ值:0。虽然λ=-0.233是最佳变换,但这种变换的实际意义不明显,考虑取其最临近的值(λ=0)变换,根据Box-Cox变换公式,λ=0即对数变换。
分析>>分布:将“白细胞”、“白细胞X”(λ=-0.233的变换数据)、“白细胞X2” (λ=0的变换数据)选入Y列,确定。
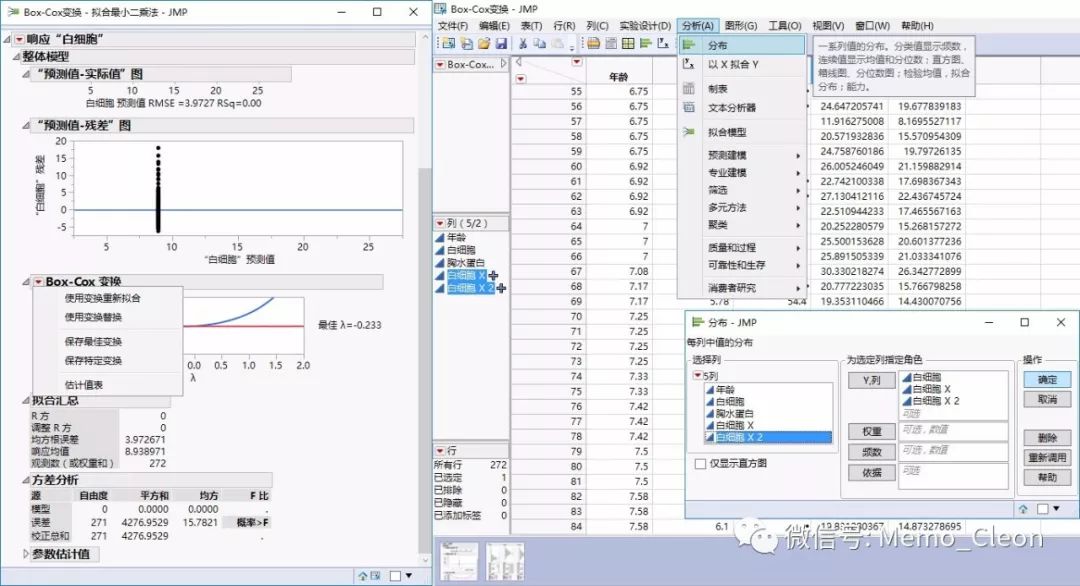
然后按本例开始时进行正态分布检验的步骤,依次通过“白细胞”、“白细胞X”、“白细胞X2”旁的红三角菜单显示正态分位数图,连续拟合正态,“正态拟合”旁红三角菜单选中拟合优度,结果如下:
经变换后数据点全部收敛在95%置信限内说明,说明变换后的数据已经服从正态分布,拟合优度检验P值均>0.05,数据服从正态分布,且两种变换差别不大。
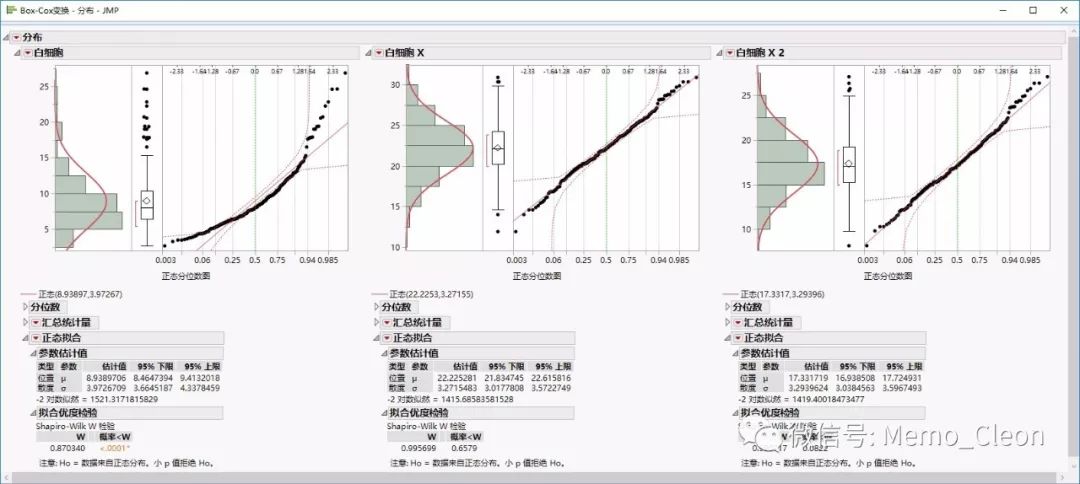
原始数据与对数变换(λ=0)的结果比较放大显示如下:
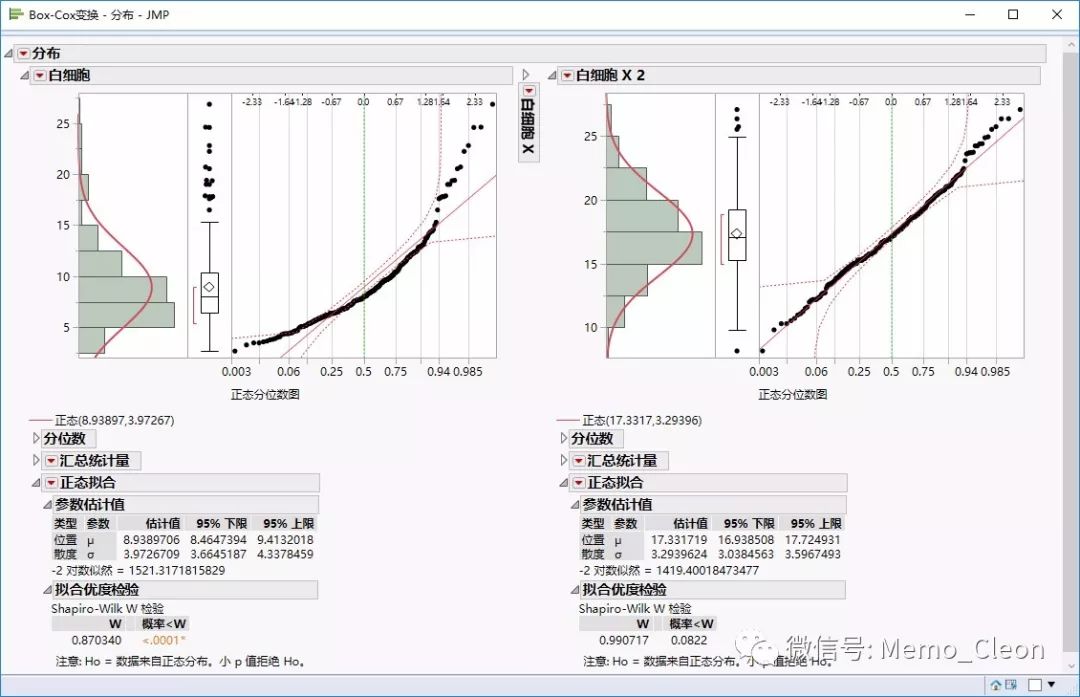



来自外部的引用