在分类预测中,我们一般比较关注准确率,但是,混淆矩阵也是非常重要的。尤其是当我们都其中的某一类别特别感兴趣的时候,通常要单独的看这个类别的召回率和精度,比如在癌症诊断过程中,我们宁愿错误的认为一个人是癌症,也不愿意把一个癌症错误的认为是正常人。本文以二元分类为例,分析ROC曲线及相关知识。
1、混淆矩阵
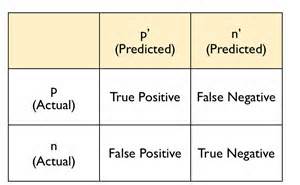
混淆矩阵如下图所示,就是把实际的类别和预测类别做一一对应,看看各个类别下正确预测了多少,错误预测了多少。在一些不平衡数据集中,一般认为稀有类别更有意义,通常计为正类,比如根据一系列指标,判断一个人是否是癌症,这种数据集中,癌症的人数是少数,即稀有类,标为正类。
在混淆矩阵中,有一些比较常用的量,但是不同的教材翻译也不一样,我一般都直接使用英文来理解混淆矩阵里的量,中文翻译里,我用的比较多的是召回率和精度。这个矩阵也比较容易记忆,就是预测的结果是P(positive)和N(negative),如果符合实际值就是T(True),不符合实际值就是F(False)。因此FN是指false negative,也就是错误预测为负样本的数(实际应该是正样本)。所以,组合成了里面的各个字符,比如TP,TN等等。那么准确率就是分类正确(即以T开头的)的除以总数,即(TP + TN)/(FP + TN + FP + FN)。这里额外说一些指标,也方便复习。
- 特指度(specificity),即真负率(true negative rate) TNP = TN / (TN+FP), 是指被模型正确预测的负样本比例。
- 召回率(recall) r = TP / (TP + FN),度量了被分类器正确预测的正样本比例。
- 精度(precision) p = TP / (TP + FP),指在分类器断言为正类的样本中实际为正类的比例。
在分类过程中,我们通常都可以通过调整阈值来调整这些值。比如还是癌症的例子,假设实际患癌症的比例是1%,使用贝叶斯分类,一般认为是癌症的比例大于0.5,就认为他是癌症。这样虽然准确率达到了最大,但是,对我们的目标而已,没有任何作用,比如我们都预测样本是非患者,那么准确率就是99%了。我们更关注癌症患者的召回率,即提高癌症患者的召回率,也就是能够把所有的癌症患者全部给预测出来。那么我们就需要降低阈值,即认为如果一个患癌症的概率大于0.1 或者0.01时,就认为他是癌症患者。这样,就会导致大量的非癌症患者被认定为癌症患者,但是同时也不容易漏掉一些真正的癌症患者。连接到混淆矩阵,就是我们提高了预测为positive的比例,使得TP和FP的都提升了,这样获得了高的召回率(小于1的正分数,分子分母都加一个正整数,分数值增大),牺牲了准确率(多数情况下,也牺牲了精度)。同样,在垃圾邮件中,我们可能会选择提供阈值,这样可以达到尽可能的不把正常的邮件认定为垃圾邮件。
我们希望构建的模型,具有很高的召回率和精度的分类模型。另外,我们也有一个度量可以把这两个指标合并在一起,即$F_1 = \frac{2rp}{r + p} = \frac{1}{\frac{1}{r} + \frac{1}{p}}$,是召回率和精度的调和平均值,会倾向于比较小的那个数。
2、ROC曲线
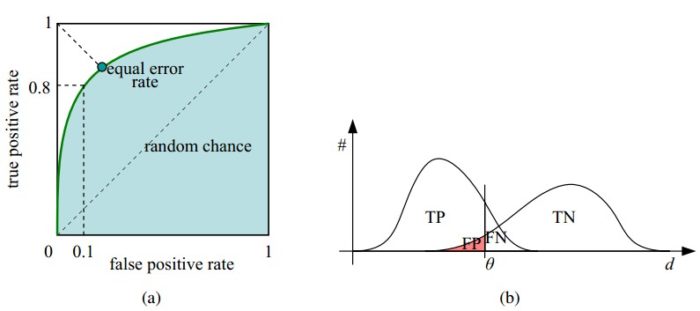
ROC曲线(receiver operating characteristic curve,受试者工作特征曲线)是显示分类器真正率(TPR)和假正率(FPR)之间折中的一种图形化方法。一个好的分类模型应该尽可能的靠近ROC曲线的左上角如果随机猜测的话,那么TPR和FPR会一直相等,最终曲线是主对角线。另外,我们也可以用曲线下的面积,来表示一个模型的平均表现。
那么我们如何绘制ROC曲线呢?思路比较简单,就是把得到的概率值和类别按照概率值排序。之后不断的调整阈值(从高到低,1到0),看看每个阈值对应的TPR和FPR,之后绘图就可以了。当然,直接使用概率值作为阈值是为了绘图的连续性。我们也可以选择阈值为0-0.1…-1.0一共11个阈值,之后计算这些阈值对应的TPR和FPR,得到十一个点,进行绘图。这里我做了两个roc的代码。第一个里面是把准确率计算在内了,这样方面我们确定最高准确率对应的阈值,当然我是想看看所有的阈值对应的准确率,所以最后用了排序。如果只是为了得到最好的,那么过程中,增加一个比较就可以了。第二个里面,纯粹是为了得到roc曲线。注意,有些时候,为了方便查看,绘图的时候坐标轴也不是非要在0和1,也可以设定为0.1-0.3等等区间。进行对比。
3、ROC代码
def roc1(scores):
# scores[0][1] is predict
# scores[0][0] is the target
m = len(scores)
pos_num = sum([i[0] for i in scores])
neg_num = m - pos_num
fp, tp = [], []
FP, TP = 0, 0
# decent the scores
scores = sorted(scores, key=lambda x:x[1], reverse=True)
accs = []
for n,s in enumerate(scores):
TP = len([i for i in scores[0:n] if i[0] == 1])
TN = len([i for i in scores[n:] if i[0] == 0])
FP = len([i for i in scores[0:n] if i[0] == 0])
accs.append([float(TP+TN)/m, s[1]])
fp.append(float(FP) / neg_num)
tp.append(float(TP) / pos_num)
fp.append(1)
tp.append(1)
# get the best theshold
accs = sorted(accs, reverse=True)
return fp, tp, accs[0]
def roc2(scores):
# scores[0][1] is predict
# scores[0][0] is the target
m = len(scores)
pos_num = sum([i[0] for i in scores])
neg_num = m - pos_num
fp, tp = [], []
FP, TP = 0, 0
# decent the scores
scores = sorted(scores, key=lambda x:x[1], reverse=True)
threshold = 1.0
for s in scores:
if s[1] < threshold:
fp.append(float(FP) / neg_num)
tp.append(float(TP) / pos_num)
if s[0] == 1:
TP += 1
else:
FP += 1
fp.append(1)
tp.append(1)
return fp, tp
scores = [[1, 0.2], [1, 0.8], [1,0.89], [1, 0.98],
[0, 0.1], [0, 0.3], [0,0.34], [0, 0.56]]
fp1, tp1, accs1 = roc1(scores)
fp2, tp2 = roc2(scores)