由于matlab具有强大的计算功能,用其统计数据功能优点显而易见,这里分享使用matlab中的boxplot的一些技巧,供大家参考。
Matlab boxplot命令
格式如下
boxplot(X):产生矩阵X的每一列的盒图和“须”图,“须”是从盒的尾部延伸出来,并表示盒外数据长度的线,如果“须”的外面没有数据,则在“须”的底部有一个点。 www.iLoveMatlab.cn
boxplot(X,notch):当notch=1时,产生一凹盒图,notch=0时产生一矩箱图。
boxplot(X,notch,'sym'):sym表示图形符号,默认值为“+”。
boxplot(X,notch,'sym',vert) %当vert=0时,生成水平盒图,vert=1时,生成竖直盒图(默认值vert=1)。 Matlab中文论坛
boxplot(X,notch,'sym',vert,whis) %whis定义“须”图的长度,默认值为1.5,若whis=0则boxplot函数通过绘制sym符号图来显示盒外的所有数据值。
箱线图(Boxplot)也称箱须图(Box-whisker Plot),是利用数据中的五个统计量:最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法,它也可以粗略地看出数据是否具有有对称性,分布的分散程度等信息,特别可以用于对几个样本的比较。
画图步骤:
1、画数轴,度量单位大小和数据批的单位一致,起点比最小值稍小,长度比该数据批的全距稍长。
2、画一个矩形盒,两端边的位置分别对应数据批的上下四分位数(Q1和Q3)。在矩形盒内部中位数(Xm)位置画一条线段为中位线。
3、在Q3+1.5IQR(四分位距)和Q1-1.5IQR处画两条与中位线一样的线段,这两条线段为异常值截断点,称其为内限;在F+3IQR和F-3IQR处画两条线段,称其为外限。处于内限以外位置的点表示的数据都是异常值,其中在内限与外限之间的异常值为温和的异常值(mild outliers),在外限以外的为极端的异常值(extreme outliers)。
4、从矩形盒两端边向外各画一条线段直到不是异常值的最远点,表示该批数据正常值的分布区间。
5、用“〇”标出温和的异常值,用“*”标出极端的异常值。相同值的数据点并列标出在同一数据
线位置上,不同值的数据点标在不同数据线位置上。至此一批数据的箱线图便绘出了。统计软件绘制的箱线图一般没有标出内限和外限。
箱线图的功能
箱线图作为描述统计的工具之一,其功能有独特之处,主要有以下几点:
1.直观明了地识别数据批中的异常值
一批数据中的异常值值得关注,忽视异常值的存在是十分危险的,不加剔除地把异常值包括进数据的计算分析过程中,对结果会带来不良影响;重视异常值的出现,分析其产生的原因,常常成为发现问题进而改进决策的契机。箱线图为我们提供了识别异常值的一个标准:异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值。虽然这种标准有点任意性,但它来源于经验判断,经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知,基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的,但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的,而均值和标准差的耐抗性极小,异常值本身会对它们产生较大影响,这样产生的异常值个数不会多于总数0.7%。显然,应用这种方法于非正态分布数据中判断异常值,其有效性是有限的。箱线图的绘制依靠实际数据,不需要事先假定数据服从特定的分布形式,没有对数据作任何限制性要求,它只是真实直观地表现数据形状的本来面貌;另一方面,箱线图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的耐抗性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响,箱线图识别异常值的结果比较客观。由此可见,箱线图在识别异常值方面有一定的优越性。
2.利用箱线图判断数据批的偏态和尾重
比较标准正态分布、不同自由度的t分布和非对称分布数据的箱线图的特征,可以发现:对于标准正
态分布的大样本,只有 0.7%的值是异常值,中位数位于上下四分位数的中央,箱线图的方盒关于中位线对称。选取不同自由度的t分布的大样本,代表对称重尾分布,当t分布的自由度越小,尾部越重,就有越大的概率观察到异常值。以卡方分布作为非对称分布的例子进行分析,发现当卡方分布的自由度越小,异常值出现于一侧的概率越大,中位数也越偏离上下四分位数的中心位置,分布偏态性越强。异常值集中在较小值一侧,则分布呈现左偏态;;异常值集中在较大值一侧,则分布呈现右偏态。下表列出了几种分布的样本数据箱线图的特征(样本数据由SAS的随机数生成函数自动生成),验证了上述规律。这个规律揭示了数据批分布偏态和尾重的部分信息,尽管它们不能给出偏态和尾重程度的精确度量,但可作为我们粗略估计的依据。
3.利用箱线图比较几批数据的形状
同一数轴上,几批数据的箱线图并行排列,几批数据的中位数、尾长、异常值、分布区间等形状信
息便昭然若揭。在一批数据中,哪几个数据点出类拔萃,哪些数据点表现不及一般,这些数据点放在同类其它群体中处于什么位置,可以通过比较各箱线图的异常值看出。各批数据的四分位距大小,正常值的分布是集中还是分散,观察各方盒和线段的长短便可明了。每批数据分布的偏态如何,分析中位线和异常值的位置也可估计出来。还有一些箱线图的变种,使数据批间的比较更加直观明白。例如有一种可变宽度的箱线图,使箱的宽度正比于批量的平方根,从而使批量大的数据批有面积大的箱,面积大的箱有适当的视觉效果。如果对同类群体的几批数据的箱线图进行比较,分析评价,便是常模参照解释方法的可视图示;如果把受测者数据批的箱线图与外在效标数据批的箱线图比较分析,便是效标参照解释的可视图示。箱线图结合这些分析方法用于质量管理、人事测评、探索性数据分析等统计分析活动中去,有助于分析过程的简便快捷,其作用显而易见。
==========================================================
Matlab boxplot命令操作时,当画两列不同行数的向量时,默认无法操作。
==========================================================
这里是我今个统计数据的一个例子的代码和生产图。(12组数据,构建一个图,归为三类,用三种颜色标记,由于boxplot不能画legend,所以后面加了一个plot命令,才能将legend画在pos=1的右上角,具体数据内容与大家无关,不要死扣哟,O(∩_∩)O哈哈~)
X1=[1 2 3 4 5 6 7 8 9 10 11 12 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6];
Y2=[NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 36 14 45 4 3 9 9 9 19 26 26 5 9 14 14 82 82 82];
X2=[];
Y2=[];
.
.
.
X12=[];
Y12=[];
boxplot(Y1,X1,'symbol','o','colors','r');
hold on;
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y2,X2,'symbol','o','colors','r');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y3,X3,'symbol','o','colors','r');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y4,X4,'symbol','o','colors','r');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y5,X5,'symbol','o','colors','b');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y6,X6,'symbol','o','colors','b');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y7,X7,'symbol','o','colors','b');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y8,X8,'symbol','o','colors','b');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y9,X9,'symbol','o','symbol','o','colors','g');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y10,X10,'symbol','o','colors','g');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y11,X11,'symbol','o','colors','g');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
boxplot(Y12,X12,'symbol','o','colors','g');
axis([0,13,0,500]);
set(gca,'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
set(gca,'XTick',[0:1:13],'XTickLabel',{'','A-TM','B-TM','C-TM','O-TM','A-Nt','B-Nt','C-Nt','D-Nt','A-Ct','B-Ct','C-Ct','D-Ct',''});
a=plot(0:0,'r');
b=plot(0:0,'b');
c=plot(0:0,'g');
legend('TM:transmembrane','Nt:N-terminus','Ct:C-terminus');
hold off;
这是最后的生成图:



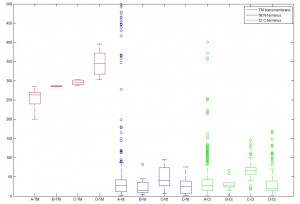
1F
我对matlab只有一点了解,用它来作过图,现想请教boxplot函数能否添加画平均值线(或’+ ‘号),如何实现。
2F
请问,为什么我的图所有数据重叠在一起