在临床研究领域,大家特别希望能够未仆先知,于是临床研究者尝试去建立各种预测模型。比如,凭借孕妇的信息预测低出生体重儿的结局。怎么建立预测模型呢?常见的做法是这样的:以低出生体重儿为因变量,以相关的孕妇信息作为自变量,建立logistic回归模型。
有了模型,一般还需要验证模型的可靠性稳定性。小编比较推荐外部验证,也就是说“用现有的数据建立模型,再收集一部分病例进行模型的验证”。其中,K折交叉验证比较常见。K折交叉验证,就是将数据随机、平均分为K份,其中(K-1)份用来建立模型,在剩下的一份数据中进行验证。比如,常见的10折交叉验证,“将数据随机、平均分为10份,其中9份用来建模,另外1份用来验证,这样依次做10次模型和验证,可得到相对稳定的模型。
说的这么热闹,怎么实现呢?SPSS可以吗?SPSS目前只是在某些模块(如决策树、判别分析)设置了交叉验证的选项,而在我们常用的线性回归、logistic回归却是没有的。小编觉得大家可以利用R软件完成交叉验证。
即使大家之前从未接触过R软件,也不难。下载、安装、运行R软件后,将小编接下来要说的程序粘贴到R控制台,改动几个参数即可。
首先,咱们需要有R软件。选择下列任意一个网站,即可链接到R下载页面。选择合适的版本,默认安装即可。
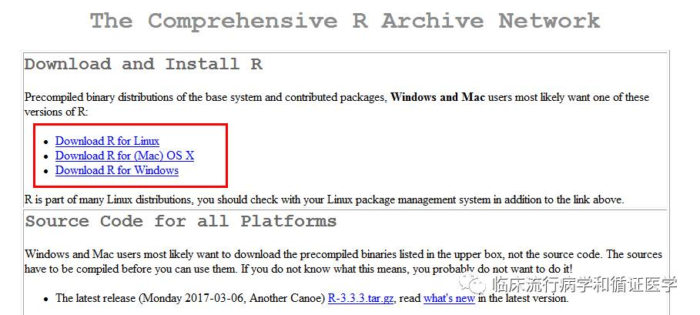
https://mirrors.tuna.tsinghua.edu.cn/CRAN/
http://mirrors.tuna.tsinghua.edu.cn/CRAN/
https://mirrors.ustc.edu.cn/CRAN/
http://mirrors.ustc.edu.cn/CRAN/
https://mirror.lzu.edu.cn/CRAN/
http://mirror.lzu.edu.cn/CRAN/
http://mirrors.xmu.edu.cn/CRAN/
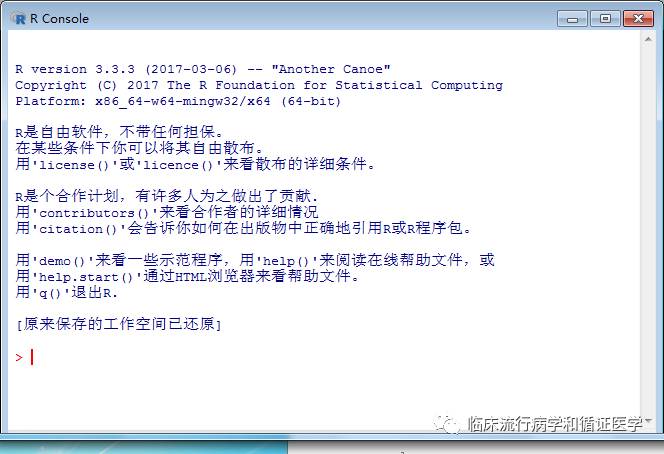
打开R是这个样子的,接下来,就是小编的程序了。
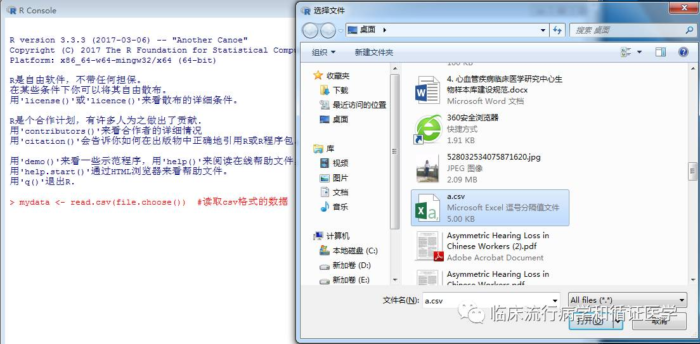
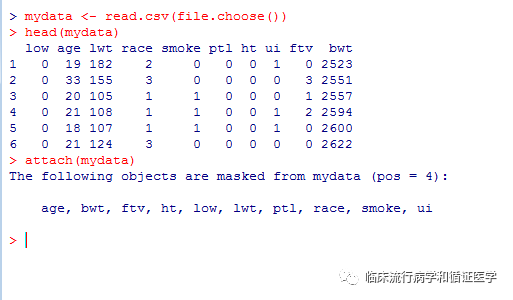
一、首先,将原始数据另存为csv格式,通过mydata<- read.csv(file.choose()) 读取数据,按下enter键,弹出选择数据的对话框,找到数据所在的位置,选择要分析的数据。
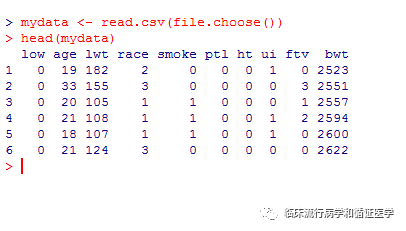
读入数据后,可通过head(mydata)查看数据前六行。
二、为了分析方便,可以将数据锁定,attach(mydata),锁定数据后可通过变量名直接引用变量。
三、因交叉验证所用的函数cv.glm在boot包里,需要下载boot包,可通过install.packages("boot"),选择国内的镜像网进行下载。

四、下载后,每次均需要加载boot包,library(boot)。
五、通过glm函数拟合logistic回归,log.fit<-glm(low~lwt ptl ht,family=binomial)。因变量为low,自变量为lwt、ptl、ht,通过family=binomia限定为logistic回归,直接键入log.fit可查看logistic回归的结果。(如果是线性回归,直接采用lm.fit <-glm(y~x1 x2 x3))
六、交叉验证时,cost默认为均方差,即(y-y预测)的平方和。所以在logistic回归模型的验证时,需要重新定义cost,意义为错判率。cost <- function(r, pi = 0)mean(abs(r-pi) > 0.5)
然后利用(cv.err<- cv.glm(mydata, log.fit, cost, K =10)$delta)求得平均错判率,这里会给出两个数值,后一个是经过校正后的错判率,因为研究者认为K者交叉验证和最初的留一验证是有偏的,结果提示平均错判率30%左右。
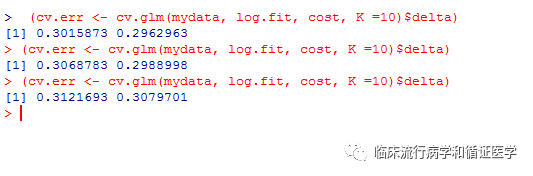
但是,为什么每次结果都不一样呢?因为,咱们是随机分成K份,cv.glm不允许用户自定义种子数,故导致每次结果略有不同。另一个安装包cvTools是可以允许用户自定义种子数,感兴趣的可以看看。文末的程序大家只需要改一改蓝色标注的,即可复制到R控制台,如运行中遇到问题,欢迎大家留言讨论。
logistic回归的交叉验证
mydata<- read.csv(file.choose())#弹出对话框,选择要分析的数据
attach(mydata)#锁定数据
install.packages("boot")#安装boot包
library(boot)#加载boot包
log.fit<-glm(low~lwt ptl ht,family=binomial)#拟合logistic回归模型
cost<- function(r, pi = 0) mean(abs(r-pi) > 0.5)#定义cost函数,计算错判率
(cv.err <- cv.glm(mydata, log.fit, cost, K =10)$delta)#交叉验证,计算平均错判率
线性回归的交叉验证
mydata<- read.csv(file.choose())#弹出对话框,选择要分析的数据
attach(mydata)#锁定数据
install.packages("boot")#安装boot包
library(boot)#加载boot包
lm.fit<-glm(low~lwt ptl ht)#拟合线性回归模型
(cv.err <- cv.glm(mydata, lm.fit, cost, K =10)$delta)#交叉验证,计算均方差


