引文
每当我使用一个新的软件/算法时(相较于组内之前的研究),导师总喜欢问我背后的原理。她可以不懂,但我必须给她讲明白。
想给一个实验背景的人,讲明白一个算法的内在逻辑,属实不易。光是一颗聚类树,我就讲了好几次,当然主要是因为我无法用通俗易懂的语言去表述
因此,我想试着用通俗易懂的语言为大家讲一下WGCNA~
Gene A的表达,可能会影响另一个基因(比如gene B)的表达。若前者是转录因子,那么多半会促进后者的转录增加;若前者是抑制子(repressor),则可能会导致后者的表达受到抑制。
随着研究的越来越深入,我们发现。这种调控关系,不是一对一的,甚至不是一对多的,而是多对多的。这里以大家耳熟能详的RNA Pol II举例,这是一个真核生物中蛋白质编码基因转录所需的RNA聚合酶。
- gene A在转录前,需要先组装一个转录前起始复合物,这个复合物是由多个基因的转录产物所组成。复合物的任何一个亚基的缺失,都会导致其靶基因(一般有很多个)的表达受到影响。同样的,转录前起始复合物的多个亚基,其对应基因的表达都会影响下游基因的转录。
好了,现在我们知道基因的调控关系是多对多的,那么我们该怎么描述这种关系呢?搞数学的那帮家伙早早的就把这玩意研究透了,用图来描述这种网络关系,也就是下面这玩意。
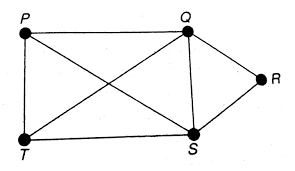
研究之透彻,光是想入门就需要先学一下离散数学,然后再上一门叫作图论的课。当然,深入学习虽然难,但是对于我们来说,只用简单的了解一下其基本概念就足以。
上面的图,我们称之为网络。网络中的每个点我们称为顶点,用于表示某个事物或者对象。其中的每条边,用于表示事物之间的关系。一个点所连接的线的个数,我们称之为度(degree)。这张网络,如果放到基因调控的背景下,其中的每个点代表一个基因,其中的每条边代表两个基因之间的调控关系。
看到这里,爱思考的朋友肯定就想到了,这个网络图似乎没有方向。这似乎和我们所了解的调控网络不太一致,于是我们这里引入有向图的概念,也就是下面这玩意。
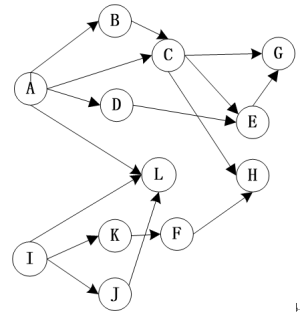
有了方向,我们就知道在一张调控网络中,究竟是gene A调控 gene B还是gene B调控gene A。但是这张图和我们想象中的调控网络还是差了点意思,调控网络中,通常是若干个基因起着重要作用,调控大部分基因,比如转录因子/蛋白激酶。而其他的大部分基因都是打酱油的,负责好自己的本职工作,再老老实实的听上游基因的调控就行了。就如下图
原谅我找不到合适的有向图,只能拿无向图代替。不过这张图可以很好的说明后续的WGCNA的网络关系
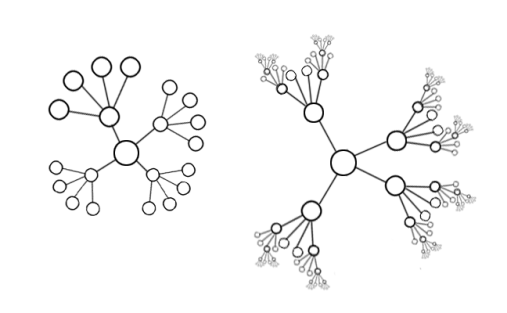
因此,在这里,我们引入一个新的概念,无尺度网络或者说是无标度网络 (scale-free network)。这是带有一类特性的复杂网络,其典型特征是在网络中的大部分节点只和很少节点连接,而有极少的节点与非常多的节点连接。
与无尺度网络对应的网络,我们一般称之为随机网络
而这类关键基因在调控网络中,因为其连通性很好(degree很高,或者说是与很多基因都有调控关系),经常会将其称呼为hub-gene。
hub是highly-connected gene的缩写
好了,讲到这里,我们基本上懂了网络的概念,以及基因调控的概念。接下来再引入基因共表达调控,就不会显的那么突兀了。
随着高通量测序技术的发展,我们可用的数据已经越来越多。传统的两两比对分析,会让我们的计算量爆炸性的增加。比如差异基因表达分析,如果我们有五个时间点的样本,两两比较就要比较4 3 2 1=10次。不仅计算量大,而且分析复杂,让本就不简单的问题更为复杂。
不一定非要是不同的时间点,也可以是不同的组织类型的发育调控
为了解决这么一个问题,我们必须利用新的方法去分析这类问题,而WGCNA就是一种刚好适合这种复杂样本的分析方法。
WGCNA全称是Weighted Gene Co-expression Network analysis,翻译成中文就是加权基因共表达网络分析。听名字我们就知道,该分析最重要的就是加权和共表达。而这个玩意最主要的目的就是帮助我们缩小范围,筛掉无用信息,找到符合我们预期的关键基因。
共表达,就是去鉴定那些高度协同变化的基因集,比如某一类基因在不同的样本中都是一起上升,一起下降,表达模式基本一致。
而加权就是在分析的时候,赋予基因共表达关系一定的权重。比如gene A和gene B的相关性更高,那这俩基因之间的权重也就越高,同样的,若二者相关性较低,则它俩之间的权重也就越低。这种加权网络,可以用下图表示,其中权重越高,则两个点之间的连线越粗。
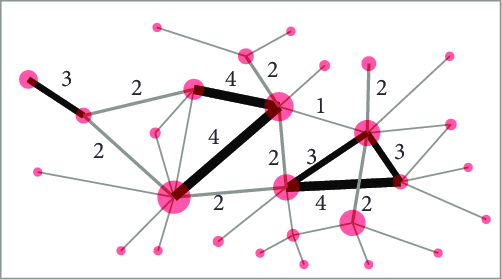
需要注意的是,基因共表达网络是一种无向图,不指定共表达关系的方向和类型。然而在基因调控网络中,边是有方向的,代表着反应、变换、互作、激活或者抑制的生化过程。而基因共表达网络并不尝试判定因果关系,边只代表基因之间的相关或者依赖关系。有类似功能或参与统一生物功能的基因会产生很多相互作用,在基因共表达网络中会体现为模块或连接丰富的子图。
Note: 基因共表达网络不具有方向性,但我们可以关注调控的正负。即,我们可以关注高度相关的基因,也可以只关注高度正相关的基因,具体的设定可以关注后续正文内容
正文
正文部分,我想尽可能的从原理出发,讲解WGCNA背后的大致逻辑。我尽可能的在这部分不介绍代码,以免喧宾夺主般的干扰我们对于WGCNA原理的思考。
先简单给个目录,WGCNA背后逻辑得讲解将从一下几个部分进行:
- 数据过滤
- 构建共表达网络
- 构建相似度矩阵
- 构建邻接矩阵的参数选择
- 构建拓扑重叠矩阵(TOM)
- 利用TOM进行聚类
- 识别基因模块
- 合并相似模块
- 模块功能的验证
- 模块与外部性转的关联
- R中的WGCNA可视化
- Cytoscape的网络可视化
数据过滤
对于想要分析的数据,我们要保证缺失值不能过多,如果过多我们必须将这些数据去除。好在我们不用手动去除,只需要交给WGCNA的一个函数即可,这样可以保证数据去除的标准更加客观。
此外,对于多个样本的数据,很有可能某几个样本与其他样本的差异太大,这将严重影响我们后续的分析。因此在前期数据过滤部分,我们首先要进行聚类,查看一下哪些样本不符合我们的预期,提前将这些样本去除。下面是一个简单的聚类结果
我一直觉得聚类可以单独写一个教程具体讲解一下,起码了解一下常见的聚类方法和原理
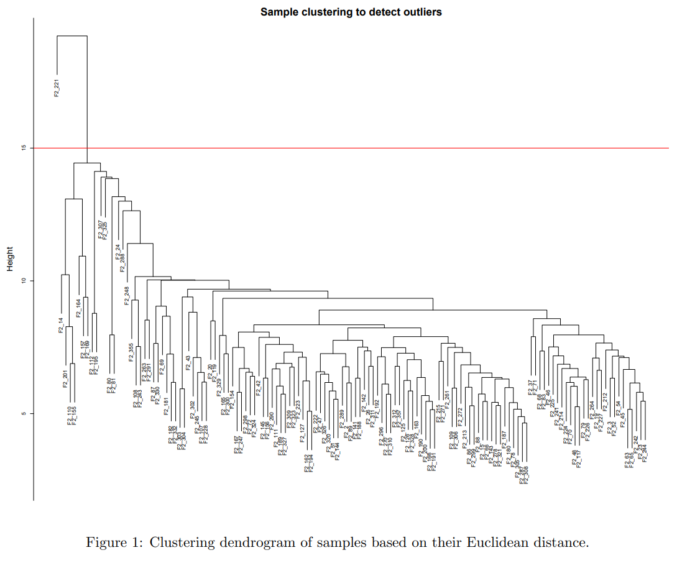
其中的红线,将样本中的outlier与其他样本区分开。这个cut-off的选取可以自己设置,将自己认为的outlier排除在外即可。
我相信即使不懂聚类的原理,也能看出来左上的那个分支所代表的样本,和其他样本相差甚远
构建共表达调控网络
这一部分是WGCNA的重头戏,不得不好好说道一下……
构建相似度矩阵
一个网络关系通常是由一个邻接矩阵所定义的,在这个矩阵中,每个元素的取值范围都在0-1之间,代表两个节点之间的连接强度。比如矩阵中第i行,第j列的元素我们称之为a ,它代表的就是gene i 与gene j之间的连接强度。
为了得到这个邻接矩阵,我们需要定义一个中间变量,共表达相似性矩阵。以下图为例:
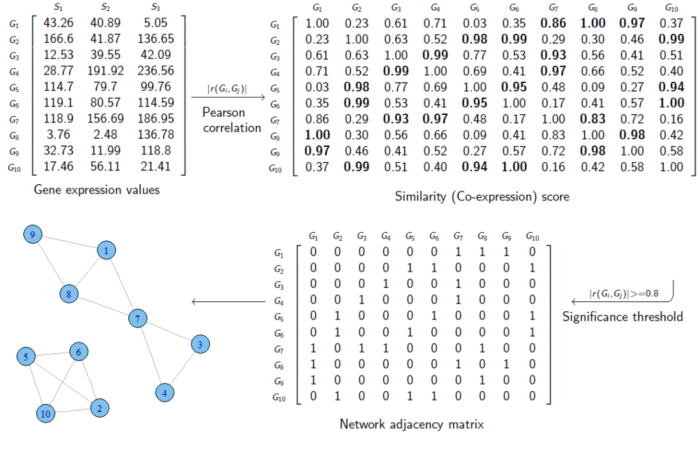
首先,我们定义一个,3样本10基因的表达矩阵。每一行是一个基因,每一列代表一个样本,每个元素代表特定样本中某基因的表达值。
有了该矩阵,我们计算Pearson相关系数,从而得到了一个10X10的相似度矩阵。这个矩阵中每个元素都代表着两个基因之间的相似度,如第三行第四列的元素值为0.99,代表Gene 3和Gene 4的相似度是0.99。
使用皮尔逊相关系数具有一个缺点,对于异常值十分的敏感。为了解决该问题,我们通常采用Jackknife相关系数,即先使用Jackknife方法进行重采样,再进行相关性的分析(先抽样,再相关性分析)
图示中的例子采用的是硬阈值(hard thresholding)的方式构建的邻接矩阵,即相似度超过0.8的才认为这俩基因之间存在连接,设置为1。而不超过0.8的则表示二者没有连接,设置为0。
硬阈值就是我们常用的一刀切的阈值
我们需要注意的是,这里定义相似度矩阵时,使用的公式是 |r(Gi, Gj)| 。即,对相关系数进行了绝对值的计算,这种方式得到的是unsigned的,即不知道是正相关还是负相关。
公式不重要,重要的是这里有一个绝对值符号;
r(Gi, Gj)的取值范围为-1到1
除此之外,我们还可以使用这个公式 |(1 r(Gi, Gj))/2| 进行计算。这样的话,我们就可以将负值(负相关)转换为正值,而原有的正值变得更大。利用这种方式,在后续分析的时候,我们更为关注的将是那些正相关的基因。
正相关反映到基因调控中,代表正向调控,gene A上调会导致gene B跟着上调
构建邻接矩阵的参数选择
最简单的一个方法,就是如上图中的例子一样,选择一个阈值(thresholding),然后一刀切。超过这个阈值的,我们认为这俩基因存在连接,低于这个阈值的我们认为这俩基因不存在链接。但是这种定义比较粗暴,比如,我定义一个cutoff为0.8,那么0.79算不算两个基因上存在连接呢?
上面那种阈值的定义方法,我们称之为硬阈值(hard thresholding)。为了避免硬阈值所带来的问题,WGCNA分析构建共表达网络时,使用软阈值(soft thresholding)。软阈值简单来说,就是将相似度进行一个幂运算,从而使得结果符合无尺度网络的标准。
该方法让原本值大的更大,小的更小。
无尺度网络模型具有一个特点就是对于部分节点的错误,具有很高程度的鲁棒性 (robustness,可以简单的理解为容错程度)。这是因为该网络具有很多的冗余链接,部分关键节点的错误并不会导致整个网络的调控出现问题。这个特点,与生物体内复杂的网络十分相似,这也是为什么使用无尺度模型的另一个重要原因。
在无尺度网络中,节点的度与该节点出现的概率是负相关的。比如:具有五个连接的节点,其出现的概率要小于有三个连接的节点出现的概率。如下图:
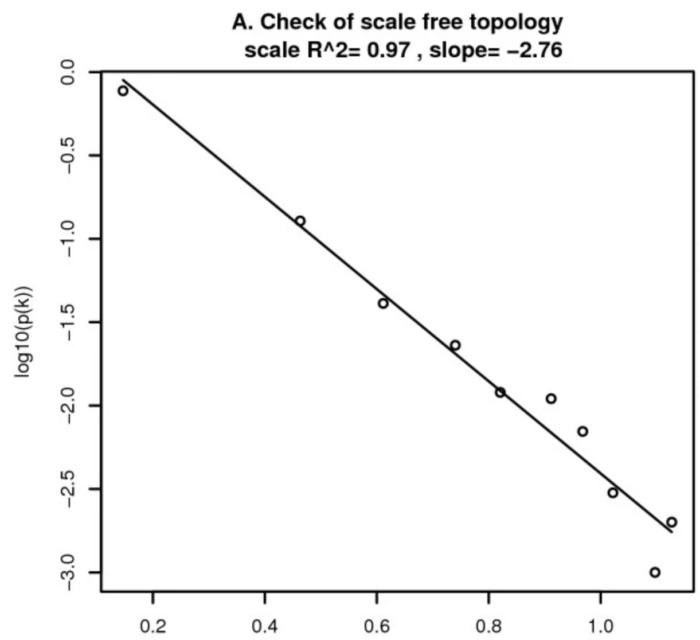
其中,横坐标表示某个节点连通性的log值,纵坐标表示该节点出现的概率的log值。当我们选择的幂指数 (power),让数据十分符合无尺度网络时,其R 就会十分的接近于1。在这张图上,分布大致遵循一条直线,这被称为近似无尺度拓扑。
连通性,简单的理解为节点上连接的边的个数
我们在使用WGCNA分析时,通常会产生一个如下所示的图辅助我们进行幂指数 (power) 的选择:
幂的英文即power,有的教程中,会使用β指代该值。
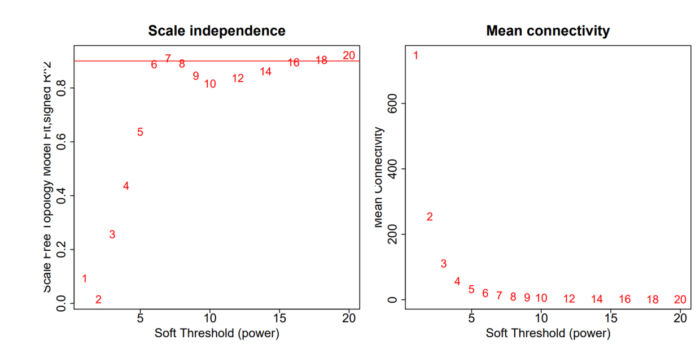
两张图的横坐标,均代表幂指数 (power) 的取值。左图的纵坐标是我们上面所讲的R ,越高越好。而右图的纵坐标代表所有节点的平均连通数,越低越好。通常我们对于幂指数 (power) 的选择主要参考左图,右图用于辅助参考。
无尺度网络中,大部分节点的连通度较低,因此平均连通数越低越好。
此外,在所有达到设定阈值的幂指数中,幂指数越小越好,不然我们直接选择1000,或者一个非常大的值它不香么?
构建拓扑重叠矩阵(TOM)
WGCNA认为邻接矩阵是不够的,基因间的相似性应该在表达和网络拓扑水平上体现。于是,又利用邻接矩阵生成了一个拓扑重叠矩阵/TOM(topological overlap matrix),此矩阵的构建还能够尽可能地最小化噪音和假阳性的影响。
gene A 与 gene B之间的关系,不仅考虑AB直接的关系,还考虑可能的多个间接关系,这样任何一个关系存在假阳性都不至于对AB之间的关系造成巨大的影响。有点无尺度网络那味了~
比如gene A 与 gene B,邻接矩阵关注的是这俩基因之间直接的共表达关系,而拓扑重叠矩阵还考虑中间因素的影响,不止关注gene A对B的调控,还要关注geneA对B的次级影响。比如gene A调控 gene C,gene C又调控gene B。
既然考虑了次级调控,为什么不考虑更次一级的调控呢?这里将其称之为三级调控。如,A不仅自己调控B,还通过调控C,C调控D,D又调控B的方式,间接的调控B。两个原因,一个可能是计算量太大,太耗费计算资源了。另一个可能是,三级调控对基因B的影响基本可以忽略不计了,这样也就可以解释为什么没有四级调控,五级调控……
那么拓扑重叠矩阵怎么计算得到呢?具体看如下公式:
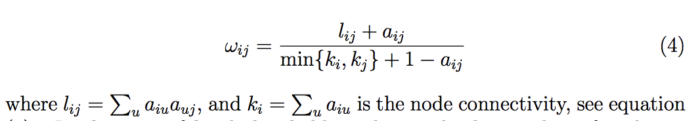
看的我脑袋疼,相信你们脑袋也疼。所以我们还是举个例子把,这样更方便大家的理解。具体如下图:
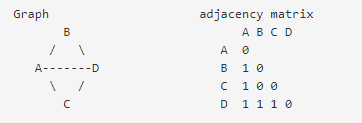
邻接矩阵中,A与D的关系是1。而在拓扑重叠矩阵中,A和D的关系,不仅需要考虑A和D之间的虚线,还需要A-B-D以及A-C-D。(通过B与C的两条间接关系)
ABBC=11,=1 ACCD=11=1,因此公式中l =1 1 = 2, a =1。l a 就是A 到D 的直接和间接共表达的总和。而我们可以知道A的k是3 (k ),D的k也是3,因此min{k ,k }=3,因此最终w 的结果为(2 1)/(3 1-1)=1,即我们得到的拓扑重叠矩阵中,第i行j列的元素值为1。
利用TOM进行聚类
有了拓扑异构矩阵(TOM)之后,我们需要进行聚类,从而对基因分块,得到不同的模块(module)。为了更好的展示聚类结果,我们用1减去TOM,从而得到对应的基因不相似性的矩阵(dissTOM)。
接着利用该不相似性的矩阵,进行聚类,聚类结果示例如下:
WGCNA直接将1-TOM得到的矩阵dissTOM,强制转换为距离矩阵。因此越相关的两个基因,其dissTOM中值越小,距离矩阵中对应的距离越近,在图中表示就是越容易聚到一起。
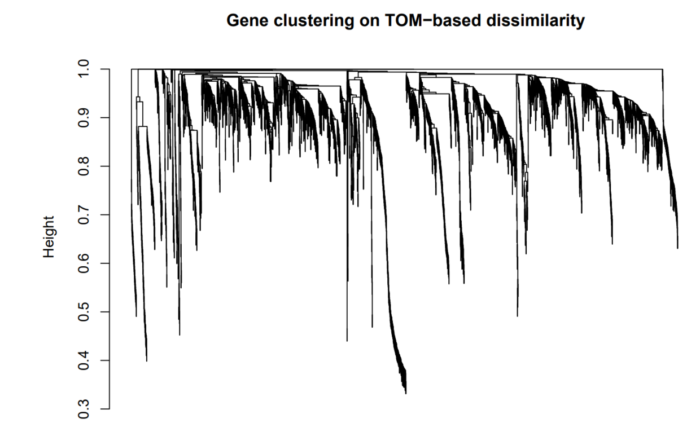
在这张图上,树上的每一个叶子节点都是一条小竖线,代表着一个基因。左侧的纵坐标(height)表示两个子节点的距离,如gene A 与 gene B 在0.75处merge到了一起,则这俩基因的距离为0.75,不相似度为0.75。
识别基因模块
得到聚类结果之后,接下来要做的就是找模块(module),即那些连接十分紧密的基因集(共表达程度很高的一类基因),聚类后的每一个簇代表着一个module。
通常将模块树的分支切分开的方法有两种,一种是指定一个高度,将结果分成若干个模块(即:数据预处理部分的红线)。另一种是使用 dynamic branch cut methods,该方法的优点是可以自动化的将module区分开,不再需要手动指定高度,且该方法更为灵活。
使用Dynamic Branch Cut方法处理得到的结果如下:
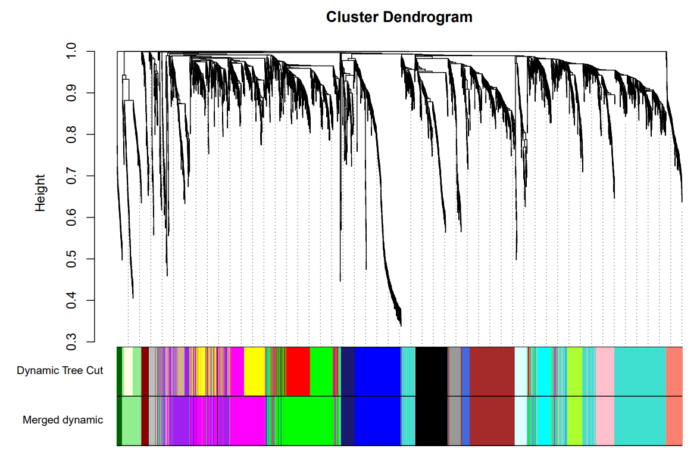
合并相似模块
Dynamic Branch Cut作为一种自动切分模块的方法,有时可能会识别出来两个表达谱非常相似的模块,此时就需要我们手动将这些高度共表达的模块合并,方便后续分析。首先需要对不同的模块进行聚类:
Dynamic Branch Cut利用形状参数确定分类的个数
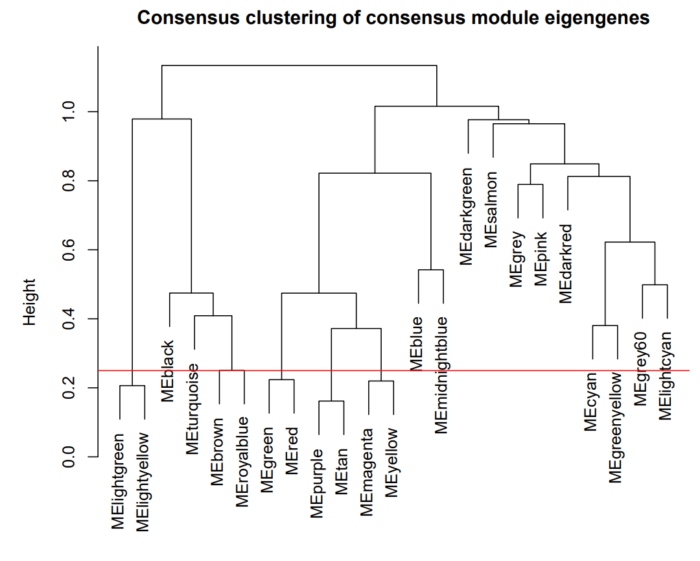
这里选择的高度为0.75,对应的相关性为0.75。表示,我们要将相关性大于等于0.75的模块进行合并,最终合并结果如下:

认真看,可以观察到,紫色和黄色两个色块合并到了一起,绿色和红色两种module合并到了一起。
模块功能的验证
层次聚类的一个缺点是很难确定究竟应该将整个数据集分成几类,尽管我们采用多种分支剪切/模块识别的方法,但是数据的分类问题,是一个开放式的探索问题,并没有一个固定解。即:合理即可。
那么怎么划分模块才是比较合理的呢?通常来说一个共表达模块反应着一个真实的生物学信号,比如通路,比如某个生物学过程。或者反应着噪音,如组织污染,技术偏差,假阳性等。
为了判断一个模块的划分是否合理,通常我们会对一个模块进行GO富集分析,判断是否富集在某一个或者某几个通路。
模块与外部性状关联
在WGCNA中,我们将划分得到的模块,与外部性状相关联,来查看每个模块分别与什么性状高度相关,从而找到我们感兴趣性状的对应模块。这些性状可以是各种指标,比如小鼠的重量,尾长,毛色等;也可以是对应植物的高矮,果实多少,颗粒饱满度等。
但是我们知道计算显著性,通常是两个向量之间作比较。但是一个模块是一个矩阵,矩阵和向量之间,计算相关性,我们该如何分析呢?WGCNA选择使用PCA的方法,计算模块矩阵的主成分,并将其中的PC1定义为eigengenes。
有了eigengennes 我们就可以计算模块与外部性状的相关性了。可视化结果如下:
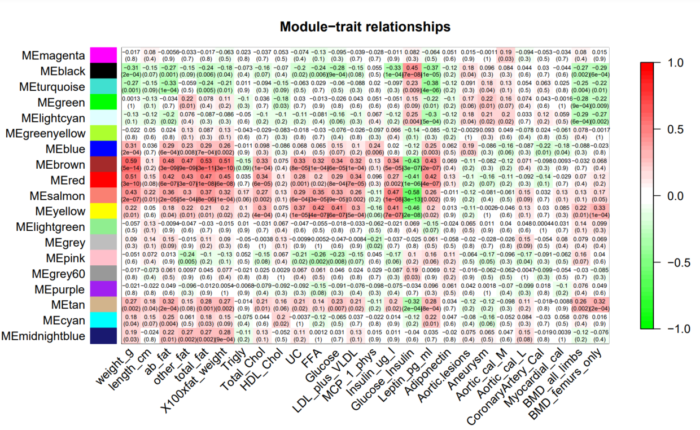
热图中的每个元素代表指定模块和对应性状的显著性,我们重点关注那些高度显著的元素,即红色的方块。
模块与指定性状的相关性我们已经分析得到了,但是一个模块通常有很多基因。我们如何找到最相关的基因呢?WGCNA通过GS和MM给出了一个合理的解决办法。
首先我们将模块中的每个基因与eigengenes进行相关性分析,得到的结果我们称之为module membership(MM)。当结果越接近于0,则我们认为该基因与其所在的模块越不相关。而结果越接近于1或者-1,则我们认为该基因与模块基因高度相关,正负表示其是正相关还是负相关。
此外,module membership与模块内的连通性是高度相关的。其中,高连通性的hub genes倾向于有更高的module membership 值。有了这个因果关系,我们不需要通过cytoscape绘制网络图,也可以找到hub genes了。
模块内的基因,我们不仅想知道它与模块的相关性,还想知道它与模块对应的性状的相关性。于是WGCNA定义了一个新的变量GS (gene significance),即计算模块内gene 与对应性状的显著性。下图展示了 module membership的相关性散点图:
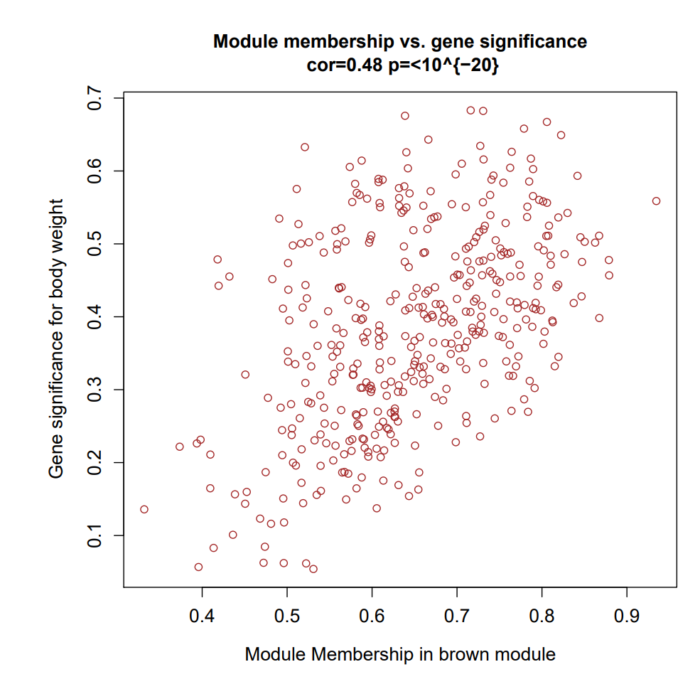
从上图我们可以看到,GS和MM还是很相关的,这表明与性状高度相关的基因,通常也是该性状对应模块内比较重要的基因。因此当我们选择感兴趣的重要基因时,推荐选取散点图右上角部分的基因。
R中的WGCNA可视化
我们通常使用热图展示我们得到的权重网络,其中每一行和每一列分别代表着一个基因。使用热图可以给我们展示哪些基因之间更为相似,通常来说都是一个模块内的基因相似度更高。如下图:
热图中方块的颜色越深(红)表示共表达相关性越高,越浅(黄)表示相关性越弱
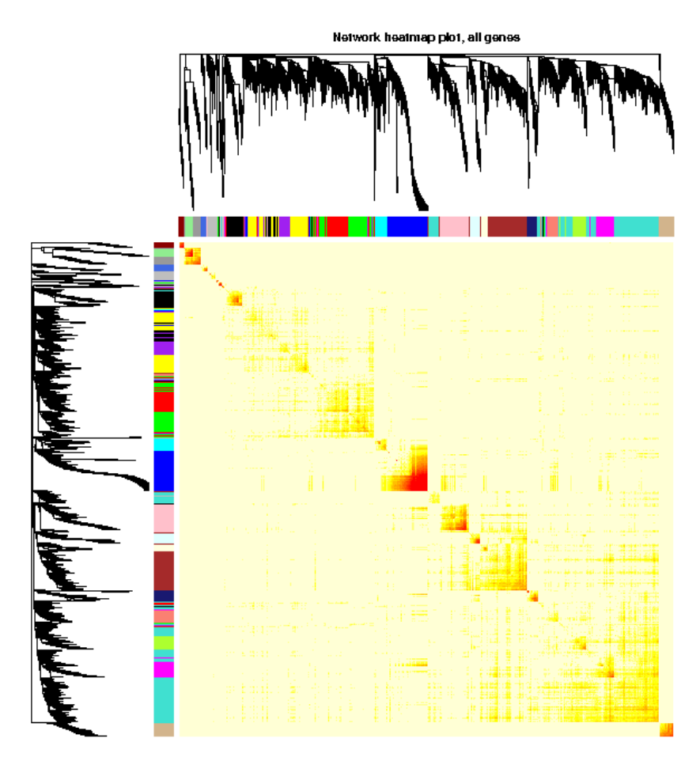
除了看基因之间的共表达程度,我们还可以看看不同模块之间的关系。这时候,就需要我们之前计算得到的eigengenes了,利用eigengenes我们可以得到不同模块的聚类,可视化不同模块的相关性,如下图:
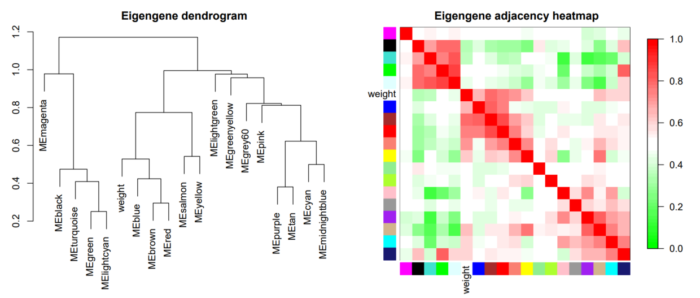
热图中,添加了weight这一外部信息,让我们看到该属性最相关的module分别是哪些。
Cytoscape的网络可视化
最后一步,也是大家最为喜闻乐见的一步,就是将我们得到的模块结果保存,并载入到cytoscape中进行网络的可视化。每个顶点代表一个基因,每条边代表两个基因之间存在共表达关系。
Cytoscape如果讲起来,那将又是一堆字,还是再单独开个教程讲解吧

完结撒花,原理/思路部分告一段落,下一部分就是WGCNA的实战部分了。实战部分将会跟着原理部分一步一步走下来,分别讲述对应的代码含义和结果。如果不想等待,而且不反感英语,强烈建议看看这个英文教程:https://horvath.genetics.ucla.edu/html/CoexpressionNetwork/Rpackages/WGCNA/Tutorials/



1F
牛牛大佬,就是有你这样的大佬存在,才让数据处理这一板块不再深奥难懂