重复测量设计是医学研究中十分常见的一种试验设计,最常见的是对同一对象在不同的时间点上指标进行测量,同一个体不同部位的指标测量也属于此类设计。重复测量数据往往不具有独立性,反应变量可以是连续型的计量资料,也可以是分类资料。分类资料的重复测量数据需要用到更为复杂的广义方程估计等广义线性模型等方法,本次学习笔记只介绍相对简单的计量资料重复测量设计的方差分析。
理论适用条件:(1)因变量之间存在相互关系:组内重复观测结果之间存在一定程度的相关性(组内样本不独立,但组间样本是相互独立的);(2)因变量均值服从多元正态分布。实际操作中往往弱化成各因素在各水平上的数据是否服从正态分布。因变量服从多元正态分布,则每个因变量分布(多元正态分布的边际分布)必然服从正态分布,反过来则未必成立,只要有一个因变量不服用正态分布则联合分布肯定不服从多元正态分布;(3)因变量方差协方差矩阵齐同。方差协方差矩阵简称协方差矩阵。一元方差分析分析的是方差,多元方差分析分析的是方差协方差。
重复测量设计的方差分析有两种方法:一元方差分析和多元方差分析。
一元方差分析要求:样本随机、正态、组间方差相等、原始资料符合H型协方差矩阵(协方差矩阵球形对称或复合对称)。是否满足球对称,常用Mauchly球性检验。Mauchly球性检验检验统计量卡方。资料满足H型协方差矩阵,说明重复测量数据实际上不存在相关性,可以采用一元裂区方差分析,若不满足则需要对自由度进行校正,校正系数ε有三种方法。
多元方差分析要求:各反应变量服从多元正态分布、组间方差-协方差矩阵齐同、各因变量存在一定的关联。组间方差-协方差矩阵齐同需要进行Box’M组间方差-协方差矩阵齐性检验。
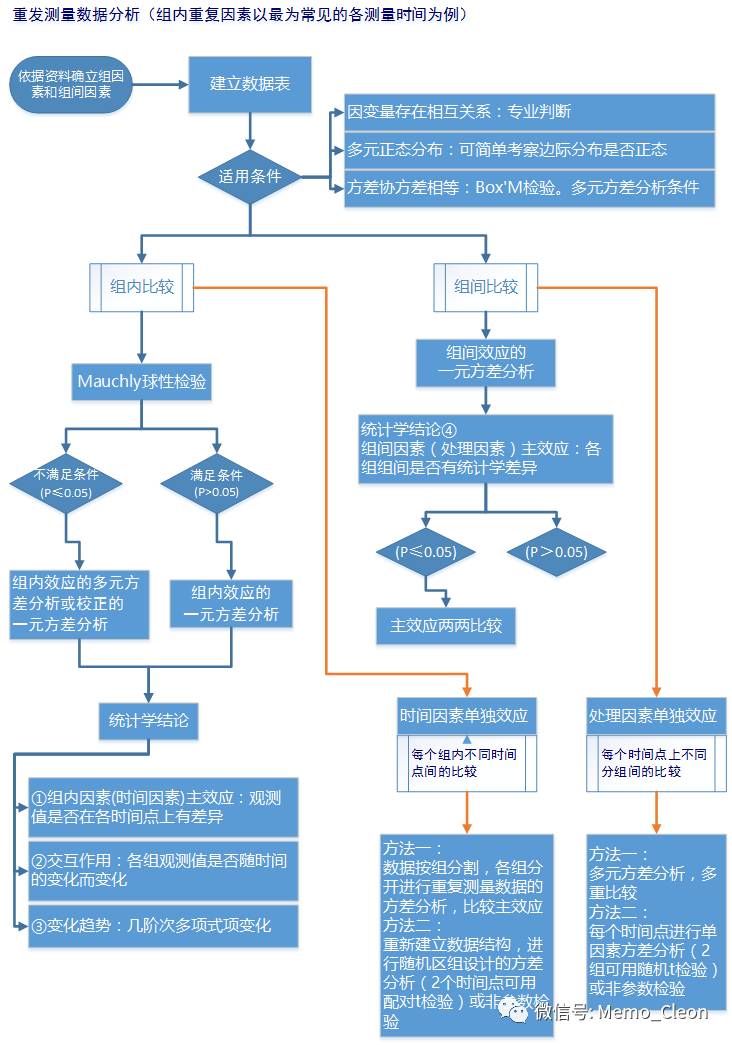
示例:slit与安慰剂治疗过敏性鼻炎的疗效研究(指标为过敏性鼻炎的症状积分)
(1)数据录入,变量视图如下,数据视图略
(2)多元方差分析对多元正态分布的要求不高,实际常弱化成各因变量边际正态分布考察,可用Explore等过程,具体操作略。
(3)分析(Analyze)>>一般线性模型(General Linear Models)>>重复测量(Repeated Measures…)
重复测量因素定义对话框:
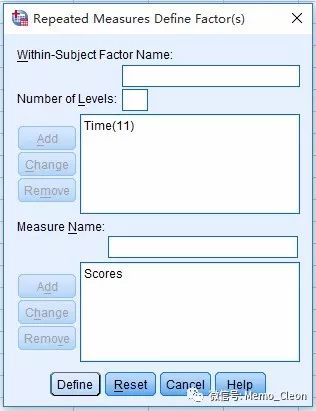
受试者内因素名称(Within-Subject Factor Name):组内因素名称,本例组内因素为11个时间点,命名为Time
水平数(Number of Levels):11
点击“添加(Add)”按钮
测量名称(Measure Name):本例测量的是过敏性鼻炎的症状评分,命名为Scores
点击“添加(Add)”按钮。
多变量分析时可继续添加其他变量。
点击“定义(Define)”按钮,进入重复测量对话框
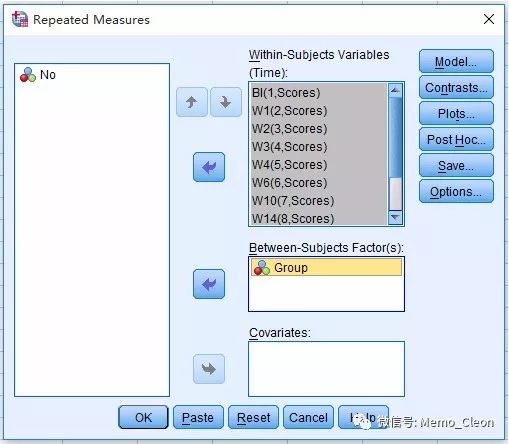
受试者内变量(Within-Subject Factor Variables),组内因素,可将左侧列表中的各个时间点对应选入该对话框
受试者间因素(Between-Subject Factors),组间因素,本例为Group。单组重复测量资料(如没有对照组的前后测量设计),该处可以不选入变量
- 模型(Model)…跟单变量方差分析类似,只是区分组内和组间因素。默认进行全因素分析
- 对比(Contrasts)…
默认对重复测量因素(Time)进行多项式比对检验,可用于分析测量因素(症状评分)随时间的变化趋势,最好结合轮廓图说明。其他比对选项及对应意义可参见“群殴之方差分析”中随机区组设计的方差分析
- 绘图(Plots)…
常结合趋势检验查看变化趋势和交互作用,不平行说明存在交互作用。本例Time选入水平轴(Horizontal Axis),Group选入单独单图(Separate Lines),单机添加(Add)
- 多重比较(Post Hoc)…用于多组间主效应的两两比较。本例只有两组,不需要使用该项
- 保存(Save)…
产生残差、预期值等数据
- 选项(Option)…
估计边际均数、主效应比较、描述统计量方、齐性检验、残差图等诸多内容。本例选中齐性检验(Homogeneity tests),可对方差协方差矩阵齐性进行检验(Box'M检验),同时输出各组在不同时间点上的方差齐性结果。
估计边际均数是剔除其他变量影响时算出的用于比较的各水平均值估计值,单因素模型和包含全部交互项的全模型,边际均值等于各样本均值,但含有协变量和去掉交互项的模型,边际均值和样本原始均值并不对应。若没有交互效应,各因素的作用可以直接用主效应来解释,但如果存在交互作用,主效应不能反应该因素的真实效应。因素和因素交互作用框中Overall是指估计所有样本的边际均数;后面是按各因素(本例有Group、Time以及交互项Group*Time)估计边际均数。可将组内因素Time选入显示均值对话框,选中比较主效应的复选框,进行任意两个时间点间的比较。但要注意分析前进行数据分割,不分组直接用所有的数据进行比较往往不是研究者所关注的。
- 粘贴(Paste)…
程序语句编辑器,修改或者编写分析语句。SPSS重复测量数据常遇到不等距数据(SPSS默认等距操作),本例WSFACTOR=Time 11 Polynomial (0 0.143 1 2 3 5 9 13 17 21 24)【注:0.143≈1/7周】
结果及解读
(1)各因变量分别服从或近似服从正态分布(图表略)。
(2)重复测量数据方差分析结果部分一开始给出了组间和组内因素的基本信息(图表略)。
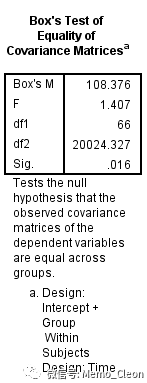
(3)Box'M组间方差协方差矩阵齐性检验结果如下:P=0.016<0.05,并不符合多元方差分析的条件。样本量较大时,Box'M检验P值会很小,且该检验对多元正态分布较为敏感,实践中也很少碰到检验不显著的情况,因此在实际应用时很多人并不会因此限制重复测量数据的方差分析的使用。
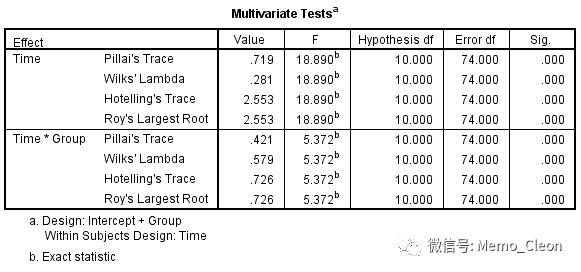
(4)组内因素多元方差分析结果:研究给出了组内因素Time、组内因素与治疗方法交互作用(Time*Group)的多元方差分析结果,分别都有4个统计量,其中Pillai'Trace最为稳健,本研究检验结果一致,当结果不一致时,以Pillai'Trace结果为准。
组内因素(Time)的主效应:P<0.001,不考虑分组,不同时间点上症状评分是不同的(至少有一个时间点的总平均值不同于其他时间点的总平均值);
Time*Group交互作用:P<0.001,时间和分组存在交互作用,时间因素的作用随分组的不同而不同。
笔者注:轮廓分析也称概貌分析,是重复测量数据方差分析的重要内容,所谓轮廓分析就是比较 分组样本的在各个时间点上均值轮廓的相似性(变化趋势是否一致,各个时间点上的轮廓距离是否相等)、重合性(组间是否有差异,轮廓距离是否足够近)、水平性(不同时间点的观测值是否有差异)。
①组内因素主效应的考察不考虑组间因素(分组因素),以组内的时间点进行分组,考察不同时间点的观测值有无差异,针对的是某个时间点上所有组的所有样本,分析结果解决的是轮廓分析中水平性问题。当存在组间因素(如本例组间因素为Group,分为slit组和plcebo组)时,这种不考虑分组的合并分析结果并不是研究者所关心的,研究者更关心的是每个组内各个时间点的比较结果,也就是对不同的分组而言,不同的时间点上的观测值是否有统计学意义或者与治疗前相比第几个时间点开始有统计学意义。分析方法是在分析前将数据按组分割,按单组重复测量资料输出结果即可。
②交互作用解决的轮廓分析中的变化趋势一致性问题。从图形上理解交互作用,笔者以为可以理解为两条趋势线不平行(变化趋势不一致),也就是在不同时间点上两组观测值的距离是不相等的(等价于不同分组在 各个时间点上观测值的变化幅度 不同)。
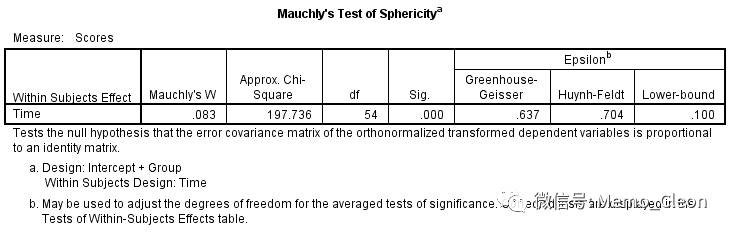
(5)Mauchly球对称检验结果:χ2=197.736,P<0.001,不满足采用一元方差分析对球性对称的假设,需要对自由度进行校正。当球性条件满足时一元方差分析的结果效能更高,直接采用一元方差分析的结果;当球性条件不满足时,则以多元分析结果为准、校正的一元方差分析结果作为补充,但如果校正的一元方差分析结果与多元方差分析结果不一致时,则以多元方差分析结果为准。
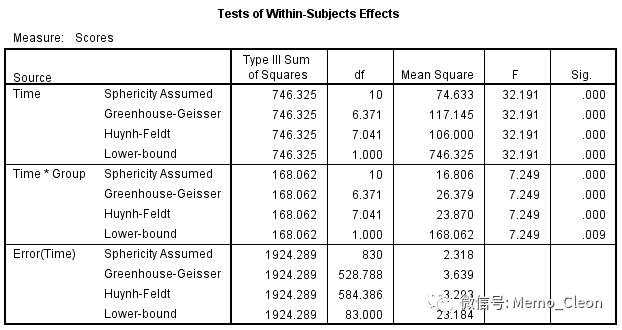
(6)组内因素一元方差分析结果:结果给出了满足球性对称时的结果和不满足球对称时的三种自由度校正结果(校正方法是自由度乘以上标中的Epsilon校正系数)。本例不满足球性假设,需要看后面三种校正的检验结果。若校正结果不一致,一般推荐Greenhouse-Geisser结果。分析结果的解读与上面的多元方差分析结果类似。
(7)组内因素趋势比对分析结果:各个测量值随测量次数(时间)的变化趋势分析结果,进一步确证组间是否存在时间趋势差异。同多元方差分析,当存在分组因素时,不考虑分组,症状积分在不同时间点的变化趋势分析结果意义并不大,研究者更关注的是不同组的变化趋势。对于不同的治疗方案,症状积分随时间的变化曲线具有不同的趋势(F=26.140,P<0.001)。
分析实际上是对拟合方程各阶次系数进行检验,H0假设分别是各阶次的回归系数=0。先进行一阶多项式(线性趋势模型)部分的分析,然后依次进行二阶多项式(抛物线性模型)部分、三阶多项式部分……的分析,重复n次测量可最高配合到n-1阶多项式。SPSS结果输出行各阶多项式系数的检验结果,首先看最高阶次的参数是否有统计学意义,如有则认为曲线间具有不同的趋势,如无则应对次高阶次的参数进行评估,如所有阶次的参数都无统计学意义,则说明曲线变化趋势一致。趋势比对的多项式分析不必要求协方差矩阵满足球性条件。
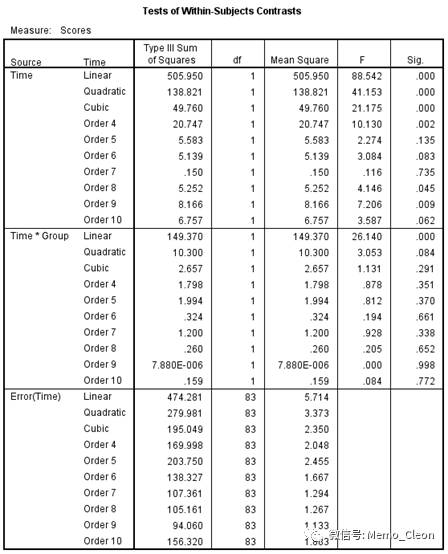
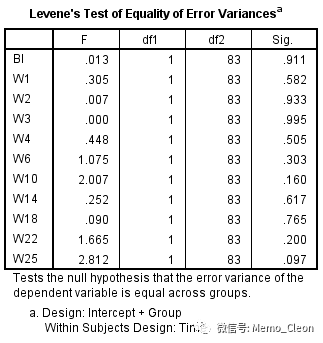
(8)单变量组间方差齐性Levene‘s检验结果:不同时间点上测量值的方差均相等。
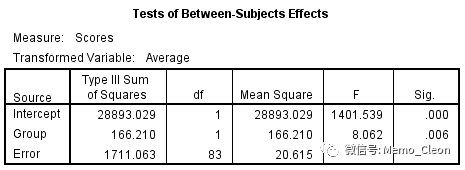
(9)组间效应的一元方差检验结果:
组间因素(Group)的主效应:F=8.062,P=0.006<0.05,采用slit和安慰剂治疗过敏性鼻炎对症状评分的改善是不同的。
组间主效应结果结合交互作用的结果解决的是轮廓分析中重合性的问题。当不存在交互作用时(趋势无差异),处理因素(组间因素)的作用可以直接用组间主效应来表示:若组间主效应存在差异表示两组不同(图形上是两条平行或接近平行的趋势线),若组间主效应没有差异表示两组相同(图形上是两条重合或接近重合的趋势线);当存在交互作用时(趋势有差异),组间主效应的分析实际意义已经不大(组间有差异是两条不平行趋势线,组间无差异是两条对称的交叉线),研究者需要分别研究组间因素和组内因素的单独效应,即不同的时间点上两组是否有差异,两组内各个时间点是否有差异。
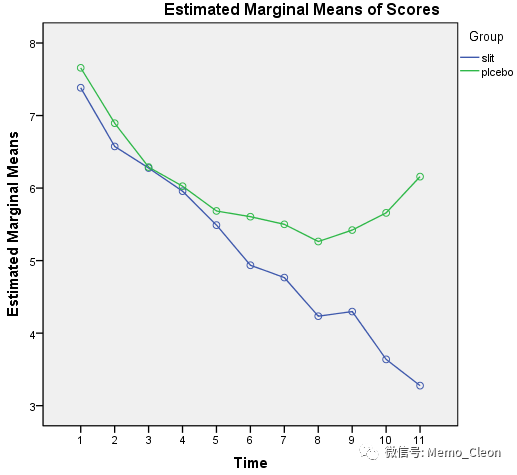
(10)轮廓图:按不同组给出了不同时间点上症状评分均数的变化曲线,slit组的评分随时间基本呈下降趋势,而plcebo组则呈现出先降后升的趋势。两组随时间变化趋势不平行,也验证了组别跟时间存在交互作用。
前面多次强调,组内因素(时间因素)的主效应往往也不是研究者所关注的,研究者更关注的是时间因素的单独效应,即每个组内不同时间点间的比较以及后续的两个时间点的多重比较。
分析方法:在进行重复测量方差分析前进行数据分割即可。
(1)数据(Data)>>数据分割(Split File)
比较组:Group
(2)分析(Analyze)>>一般线性模型(General Linear Models)>>重复测量(Repeated Measures…)
重复测量因素定义对话框同前
重复测量对话框:组内因素同前,分割数据后各组分别输出,组间因素列表不在选入任何变量
- 选项(Options)……显示均值(Display Means for)列表选入Time,选中比较主效应(Compare main effects)复选框,置信区间调整(Confidence interval adjustment):Bonferroni
粘贴(Paste)…本例WSFACTOR=Time 11 Polynomial (0 0.143 1 2 3 5 9 13 17 21 24)
其余按钮默认选项
除了在选项(Options)按钮中通过主效应进行比较,也可使用比对(Contrasts)按钮中将组内因素默认的多项式比对改为其他类型,比如simple,可将各水平与参考水平(如第一水平)做比较
结果如下:
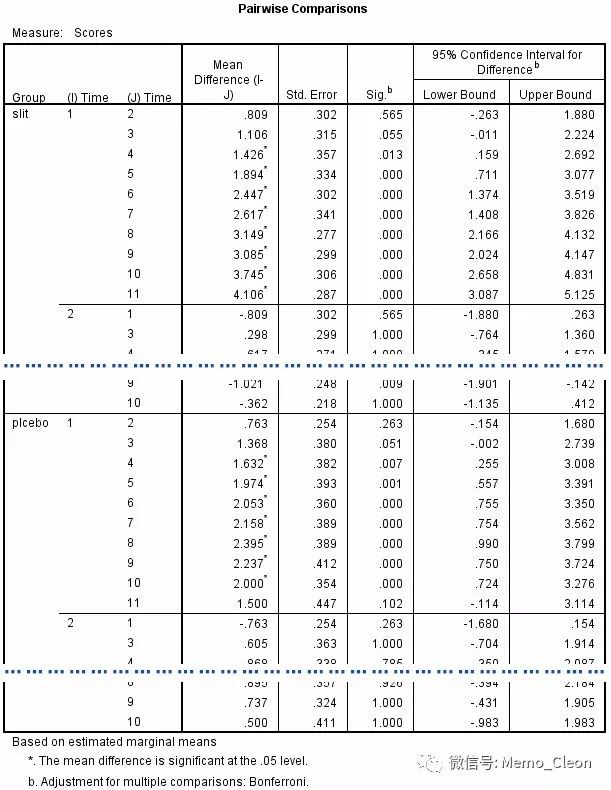
不论是slit组还是plcebo组,不同时间点上的症状评分差异均有统计学意义。
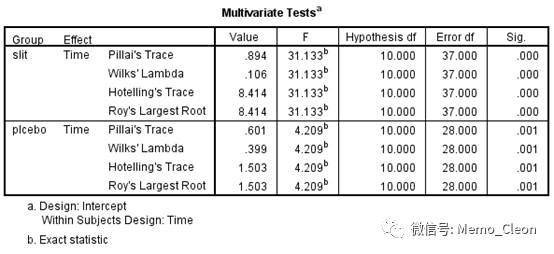
Mauchly球对称检验结果:两组P均<0.001,均不满足采用球性对称的假设,都需要对自由度进行校正。
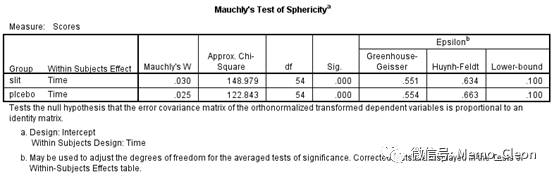
组内因素一元方差分析结果:两组的校正结果一致,P均<0.001,不同时间点上的症状评分均不同。
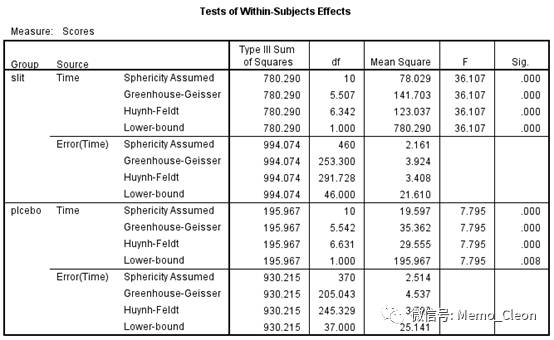
趋势比对分析结果:slit组和placebo组在多个阶次的多项式部分均有统计学意义,slit在各个时间点上症状积分的平均水平是不相等的,变化趋势可结合轮廓图进行描述。placebo组同slit。
各组各个时间点间的成对比较结果如下表,结果一目了然,不再赘述。
另外,除了趋势差异(交互作用)和组间差异(组间主效应)外,研究者可能还比较关注组间因素(处理因素)的单独效应,即每个时间点上不同分组间的比较以及进一步的两两比较。
(1)数据(Data)>>数据分割(Split File):分析所有样本,不创建组
(2)分析(Analyze)>>一般线性模型(General Linear Models)>>多变量(Multivariate)
自变量列表:选入各个时间点变量
固定因素:本例为Group
当然这一部分每个时间点间的两两比较也可以使用单变量的方差分析One-Way ANOVA或Univariate过程。
结果首先给出了多元方差分析整体分析结果:4个统计量的P值均<0.001,slit和placebo两组的症状积分是不同的。
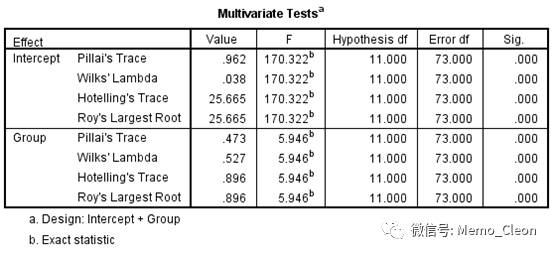
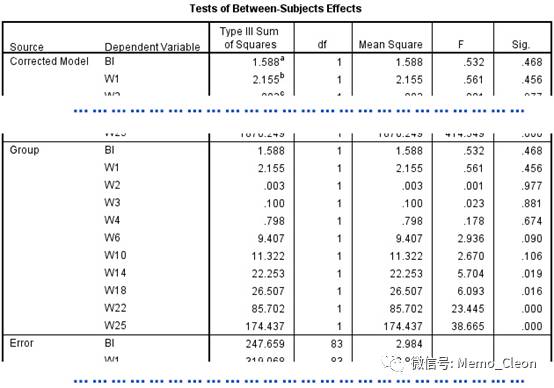
组间不同时间点上的比较结果:从第14周(W14)开始,slit和placebo组之间的症状评分开始有统计学意义。
END



来自外部的引用