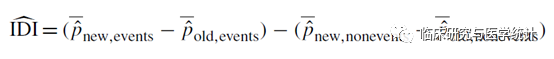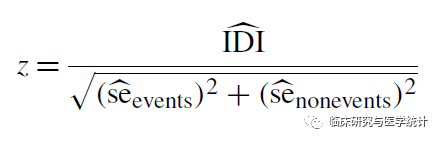题记:这一章讲综合判别改善指数(Integrated Discrimination Improvement, IDI)计算原理与方法。这个指标也用于判断预测模型改善情况,与NRI有类似也有不同,请各位斧正。
1. 背景知识
上一章《预测模型系列 07--净重新分类指数(NRI)的计算原理与方法》我们比较了ROC分析曲线下面积与NRI,NRI有两个优点:1. 较ROC分析计算的C-Statistics/AUC更为敏感;2.NRI用于在设定的cut-off值下,例如某个指标的诊断截断值或低、中、高风险划分的界值等,来比较新、旧模型的预测能力是否有所提高,在实际临床应用中更容易理解。但NRI也有一些不足:它只考虑了设定某个切点时的改善情况,不能考察模型的整体改善情况,此时我们可以选择另一个指标:综合判别改善指数(IntegratedDiscrimination Improvement, IDI)。有的读者可能会提出疑问:C-Statistics/AUC不就是反应模型整体改善情况的吗?这个问题又回到我们上一章提到的C-Statistics/AUC的两个局限性的问题,如果一定要把IDI与C-Statistics/AUC比较,那么IDI更敏感,临床也更容易解释。
我无法从一个读者的角度判断我上面这段话讲得是不是“可以听懂的人话”?但有一个最简单的解决办法:先存疑不论,即不去计较C-Statistics/AUC、NRI、IDI的优劣,在进行两个指标诊断效能比较或两个预测模型比较时,除了传统的ROC曲线计算AUC,也可以同时给出NRI和IDI,更加全方位、立体的展示新模型的改善情况,犹如绘画技法中的多点透视。
2. IDI计算原理
从IDI的计算公式看,它反映的是两个模型预测概率差距上的变化,因此是基于疾病模型对每个个体的预测概率计算所得。它的计算公式为:
其中Pnew,events、Pold,events表示在结局事件发生组(患病组)中,新模型和旧模型对于每个个体预测疾病发生概率的均值,两者相减表示预测概率提高的量。对于患病组来说,预测患病的概率越高,表示模型越准确,因此,Pnew,events与Pold,events差值越大则提示新模型越好。
而Pnew,non-events、Pold,non-events表示在结局事件发生组(未患病组)中,新模型和旧模型对于每个个体预测疾病发生概率的均值,两者相减表示预测概率减少的量,对于未患病组来说,预测患病的概率越低,表示模型越准确,因此Pnew,non-events与Pold,non-events差值越小则提示新模型越好。
最后,将两部分相减即可得到IDI,总体来说IDI越大,则提示新模型预测能力越好。与NRI类似,若IDI>0,则为正改善,说明新模型比旧模型的预测能力有所改善,若IDI<0,则为负改善,新模型预测能力下降,若IDI=0,则认为新模型没有改善。
我们可以通过计算Z统计量,来判断IDI与0相比是否具有统计学显著性,统计量Z近似服从正态分布,公式如下:
其中SEevents为Pnew,events-Pold,events的标准误,首先在患病组,计算新、旧模型对每个个体的预测概率,求得概率的差值,再计算差值的标准误即可;SEnon-events为Pnew,non-events-Pold,non-events的标准误,是在未患病组,计算新、旧模型对每个个体的预测概率,求得概率的差值,再计算差值的标准误即可。
3. R语言实现
表1.R中可计算IDI的包
| 包的名称 | 下载地址 | 分类资料结局 | 生存资料结局 |
| PredictABEL | CRAN | reclassification函数 | 不支持 |
| survIDINRI | CRAN | 不支持 | IDI.INF函数 |
[案例]示例数据来自于survival包里自带的一份梅奥诊所的数据,记录了418位患者的临床指标与原发性胆汁性肝硬化(PBC)的关系。其中前312个患者来自于RCT研究,其他患者来自于队列研究。我们用前312例患者的数据来预测是否发生死亡。这个表中的结局变量是status,0=截尾(删失),1=接受肝移植,2=死亡。为了R语言代码解释的方便,我们首先把“死亡与否”是作为二分类变量处理。然后再考虑时间因素,当做生存资料处理。其他关于数据中各变量的具体含义可用命令:? pbc 查看。
(1) 二分类结局
代码如下:here consider pbc dataset in survival package as an example
library(survival) dat=pbc[1:312,] dat$sex=ifelse(dat$sex=='f',1,0)
subjectscensored before 2000 days are excluded
dat=dat[dat$time>2000|(dat$time<2000&dat$status==2),]
predcitingthe event of ‘death’ before 2000 days
event=ifelse(dat$time<2000&dat$status==2,1,0)
standardprediction model: age, bilirubin, and albumin
z.std=as.matrix(subset(dat,select=c(age,bili,albumin)))
newprediction model: age, bilirubin, albumin, and protime
z.new=as.matrix(subset(dat,select=c(age,bili,albumin,protime)))
glmfit (logistic model)
mstd=glm(event~.,binomial(logit),data.frame(event,z.std),x=TRUE) mnew=glm(event~.,binomial(logit),data.frame(event,z.new),x=TRUE)
Using PredictABEL package
library(PredictABEL) ## Loading required package: Hmisc ## Loading required package: lattice ## Loading required package: Formula ## Loading required package: ggplot2 ## Attaching package: 'Hmisc' ## The following objects are masked from 'package:base': ## ## format.pval, units ## Loading required package: ROCR ## Loading required package: gplots ## Attaching package: 'gplots' ## The following object is masked from 'package:stats': ## ## lowess ## Loading required package: epitools ## Attaching package: 'epitools' ## The following object is masked from 'package:survival': ## ## ratetable ## Loading required package: PBSmodelling ## ----------------------------------------------------------- ## PBS Modelling 2.68.6 -- Copyright (C) 2005-2018 Fisheries and Oceans Canada ## ## A complete user guide 'PBSmodelling-UG.pdf' is located at ## C:/Program Files/R/R-3.5.1/library/PBSmodelling/doc/PBSmodelling-UG.pdf ## ## Packaged on 2017-12-19 ## Pacific Biological Station, Nanaimo ## ## All available PBS packages can be found at ## https://github.com/pbs-software ## ----------------------------------------------------------- pstd<-mstd$fitted.values pnew<-mnew$fitted.values
用cbind函数把前面定义的event变量加入数据集,并定义为dat_new
dat_new=cbind(dat,event)
计算NRI,同时报告了IDI,IDI计算与cutoff点设置无关。cOutcome指定结局变量的列序号;predrisk1,predrisk2为新旧logistic回归模型
reclassification(data=dat_new,cOutcome=21, predrisk1=pstd,predrisk2=pnew, cutoff=c(0,0.2,0.4,1)) ## _________________________________________ ## ## Reclassification table ## _________________________________________ ## ## Outcome: absent ## ## Updated Model ## Initial Model [0,0.2) [0.2,0.4) [0.4,1] % reclassified ## [0,0.2) 103 3 0 3 ## [0.2,0.4) 3 22 0 12 ## [0.4,1] 0 0 13 0 ## ## Outcome: present ## ## Updated Model ## Initial Model [0,0.2) [0.2,0.4) [0.4,1] % reclassified ## [0,0.2) 7 0 0 0 ## [0.2,0.4) 0 8 0 0 ## [0.4,1] 0 2 71 3 ## ## ## Combined Data ## ## Updated Model ## Initial Model [0,0.2) [0.2,0.4) [0.4,1] % reclassified ## [0,0.2) 110 3 0 3 ## [0.2,0.4) 3 30 0 9 ## [0.4,1] 0 2 84 2 ## _________________________________________ ## ## NRI(Categorical) [95% CI]: -0.0227 [ -0.0683 - 0.0229 ] ; p-value: 0.32884 ## NRI(Continuous) [95% CI]: 0.0391 [ -0.2238 - 0.3021 ] ; p-value: 0.77048 ## IDI [95% CI]: 0.0044 [ -0.0037 - 0.0126 ] ; p-value: 0.28396
计算的IDI为0.44%,说明新模型较旧模型预测能力仅改善0.44%
(2) 生存资料结局
代码如下:here consider pbc dataset in survival package as an example
library(survival) dat=pbc[1:312,] dat$time=as.numeric(dat$time)
定义生存结局
dat$status=ifelse(dat$status==2,1, 0)
定义时间点
t0=365*5
构建基础回归模型矩阵
indata0=as.matrix(subset(dat,select=c(time,status,age,bili,albumin)))
增加1个预测变量新模型矩阵
indata1=as.matrix(subset(dat,select=c(time,status,age,bili,albumin,protime)))
基础模型中预测变量矩阵
covs0<-as.matrix(indata0[,c(-1,-2)])
新模型中预测变量矩阵
covs1<-as.matrix(indata1[,c(-1,-2)])
dat[,2:3]设置生存结局,dat数据集第2、3两列分别是生存时间与终点。covs0,covs1,为旧模型与新模型的协变量矩阵 t0为设置的时间。npert设置迭代次数。输出结果IDI.INF计算结果:
library(survIDINRI) ## Loading required package: survC1 x<-IDI.INF(dat[,2:3],covs0, covs1, t0, npert=1000) IDI.INF.OUT(x) ## Est. Lower Upper p-value ## M1 0.025 -0.003 0.064 0.082 ## M2 0.226 -0.005 0.399 0.056 ## M3 0.012 -0.002 0.040 0.068
m1:Resultof IDI.
m2:Resultof continuous-NRI.
m3:Resultof median improvement in risk score.
计算的IDI为2.5%,说明新模型较旧模型预测能力仅改善2.5%。
IDI.INF.GRAPH(x)
4. 总结与讨论
我们用一系列文章介绍了AUC、NRI和IDI这些指标以及DCA分析在判断和比较两个预测模型预测能力中的应用,这些指标从多角度反应了模型的预测能力,我们对这三个指标再进行简单梳理:
(1).ROC分析计算的C-Statistics/AUC最为经典,也是模型区分度判断的基础。而NRI和IDI尚年轻,尽管受到越来越多研究者的推崇,但是C-Statistics/AUC的提高仍然模型预测能力改善的基础断标准。当然,我们也建议如果能够同时给出C-Statistics/AUC、NRI和IDI这三个指标则更为理想,如果能进一步做DCA分析那就更完美了。“完成”总是优先于“完美”的。
(2).如果结局指标不是二分类变量,而是多分类情况,例如低、中、高风险,那么NRI和IDI是较好的选择,AUC则较为复杂而且临床不好解释,前文已述及。
(3).NRI的计算与我们设定的cut-off点相关。如果切点划分过宽或者切点过少,NRI计算值很大可能会变小,而达不到统计学显著性,如果等级划分过窄或者切点过多,NRI计算值很大可能会变大,造成与临床意义不符合。因此,预测概率切点的划分对于计算NRI来说十分重要,一定要结合临床专业的需求来确定一个合适的切点。如果无法确定明确的划分切点,那么IDI和AUC可能是较好的选择,如果有明确的切点,那么NRI可能是较好的选择。
(4).DCA进行临床效用分析,这也是一种锦上添花的操作。除此以外,我们还要考虑一个很容易被忽视的问题,新的模型增加一个指标,那么新的模型势必比旧模型变得复杂,这种复杂模型使用者是否可以接受?比如新的指标检测是否方便?获得是否方便?获得成本高不高?这是一个利弊平衡的问题,需要研究者根据模型的改善情况与增加预测变量带来的成本之间酌情做出选择。
5. 参考文献
[1]AlbaA C, Agoritsas T, Walsh M, et al. Discrimination and Calibration of ClinicalPrediction Models: Users’ Guides to the Medical Literature [J]. Jama, 2017,318(14): 1377-84.
[2]PencinaM J, D’Agostino R B, Sr., D’Agostino R B, Jr., et al. Evaluating the addedpredictive ability of a new marker: from area under the ROC curve toreclassification and beyond [J]. Statistics in medicine, 2008, 27(2): 157-72;discussion 207-12.
[3]http://ncook.bwh.harvard.edu/r-code.html