在临床工作中,我们往往有很多决策模型可以对同一个疾病进行决策,那么谁的决策更准确呢?对于这一问题,我们往往采用AUC来判断,也就是我们会计算不通过模型的AUC,然后比较其大小。AUC大的我们认为它的结果跟金标准更一致,但是AUC有一个问题就是只关注了模型的总体准确性,并没有关注不同模型中不同切点所带来的获益与风险的关系。
除了AUC以外,我们还有NRI,即(Net Reclassification Improvement,重分类改善指标),它是用来判断我们采用不同的切点进行分类以后,改善值如何。它可以是同一个诊断方法的不同切点值,也可以是不同诊断方法的不同切点值,总之就是计算重新分类以后的改善情况。除此之外还有一个叫做决策曲线分析的方法,也可以用来解决这个问题。而且决策曲线分析还可以将不同的切点做成曲线,并画出图形,方便使用。但是需要去理解的是,决策曲线分析中引入了“阈值概率”这一概念。我们都知道ROC曲线存在切点值(又叫界值),切点值是指某指标的具体值,而阈值概率是指按切点值分类后的构成比。
比如我们用A指标来判断肿瘤,A指标的量程是1-100,且A值越大越容易得肿瘤。通过ROC曲线分析我们得知A指标的切点值是≥35,此处35就是切点值,而对应的阈值概率就等于(≥35的人数/总人数)。有了阈值概率的概念,我们再说净获益的概念,净获益是指按此概率开展措施后,因操作而获益的比例 未获益的比例*权重。决策曲线中净获益的算法如下:

下面我们通过一个具体的四格表来看一下决策曲线分析的基本计算,假设阈值概率为10%,得到如下四格表:
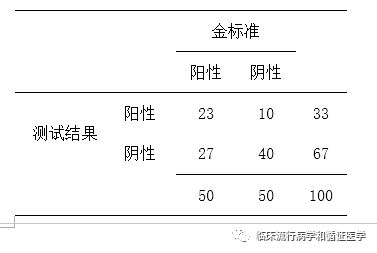
按照上面的10%的阈值去判断,我们判断对了23人,我们判断错了10人。这时候我们的净获益=(23/100)- [(10/100)*(0.1/0.9)]=0.218。同样我们可以计算当阈值概率为11%时的净获益值,也可以计算12%时的净获益值。依此类推,我们便可以获得阈值概率和净获益值的一一对应关系,还可以将此关系画成一个线图,便是决策曲线。
同样我们可以做出不同决策模型的阈值概率与净获益的线图,并把它们放在一起,便是不同预测模型的决策曲线比较。如下图,在不同的阈值概率上,那条线对应的净获益大,我们就会选择哪种方法去做。
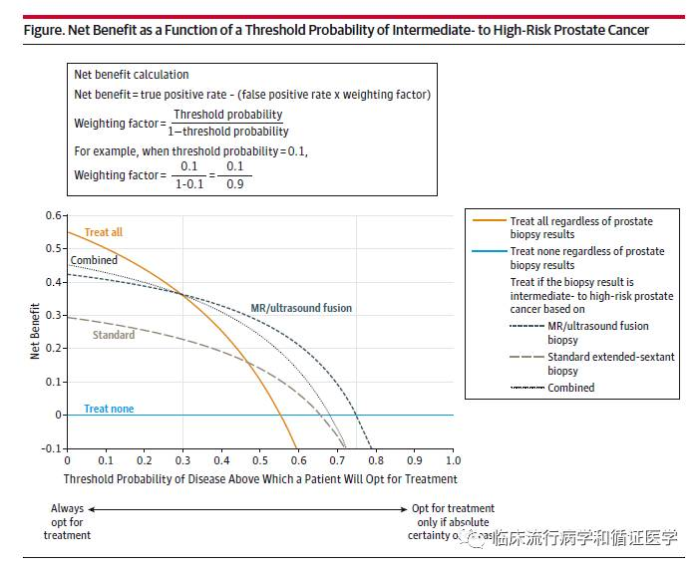
在上图中有一条蓝色线和一条黄色线,蓝色线是指所有人都不治疗,那么治疗的净获益肯定是0。黄色线是指所有人都治疗,那么净获益=金标准下的阳性率- 金标准的阴性率*(阈值概率/1-阈值概率)。当阈值概率=0时,净获益等于金标准下的阳性率,随着阈值概率的增加,其值在下降。
上面就是决策曲线的基本原理介绍,如果想了解更多内容,请访问:www.decisioncurveanalysis.org。
参考文献:
[1] FitzgeraldM, Saville BR, Lewis RJ. Decision curve analysis. JAMA. 2015; 313:409-410
[2] 肖文军, 陆茜, 姚旭东, 张世林, 戴波, 叶定伟. 决策曲线分析评价临床预测模型的应用研究. 中国卫生统计. 2012; 29: 460-461


